卡尔曼滤波器
本文主要参考该视频,在此对vic_wu表示感谢。

卡尔曼滤波器,亦称最佳线性滤波器,具有诸多优势,例如操作简便,且属于纯粹的时域滤波器,无需进行频域转换,因此在工程领域得到了广泛的应用。
若一辆汽车正于道路上行驶,我们可通过记录其具体位置与行驶速度,以描绘其即时状况,并将这些信息以矩阵格式呈现。

X(t)代表的是一个二维的列向量,该向量包含两个关键元素,分别对应汽车的两个不同状态。首先是其位置P,其次是速度V。
此外,司机还能够通过踏下油门或刹车来调节车辆的加速度,无论是向前还是向后,这种加速度用U来表示。若司机既未踩油门亦未踩刹车,则U的值为零,此时车辆将保持匀速直线前进。
若我们掌握了前一时刻的状态X(t-1),那么在这一时刻,X(t)的状态又将呈现何种情形呢?
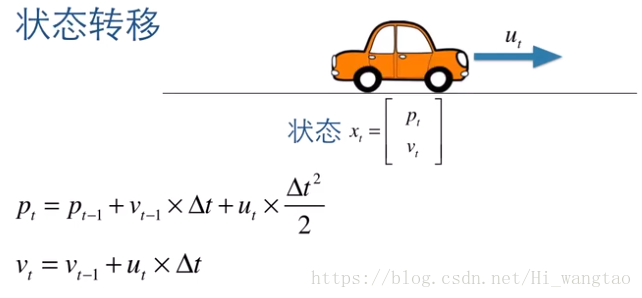
在时刻t的位置P(t)可以表示为上一时刻t-1的位置P(t-1)与速度V(t-1)相乘再乘以时间间隔(即塔T),此外,若存在加速度U(t),还需加上加速度U(t)与时间间隔(即塔T)的平方的一半。
速度的值,实际上等同于前一次速度与加速度U(t)与塔T的乘积之和,当我们仔细审视这两个公式时,可以发现它们的输出结果均仅是输入变量的线性叠加,正因如此,我们认定卡尔曼滤波器为最理想的线性滤波器。
由于它仅能展现状态与状态之间的连续性联系,既然这种联系本质上是线性的,那么我们便能够将其以矩阵的形式进行表达,呈现出如下模样。
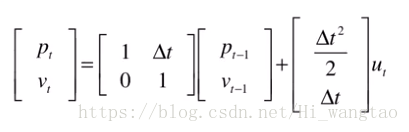
我们再进一步把两个状态变换矩阵提取出来,变成了F和B,
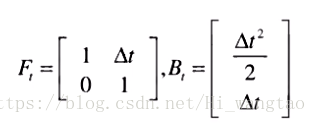
公式就可以简化成,这样。
这个公式就是卡尔曼滤波器中第一个公式状态预测公式,
其中:
F被称作状态转移矩阵,它展示了我们如何根据前一时刻的状态来推断出当前时刻的状态。
B叫做控制矩阵,他表示控制量U如何作用于当前状态。
我发现这个公式中的X似乎略有不同,它都附有一个尖角标记,这表明它代表的是对X的预测值,而非X的实际数值。由于汽车的实际状况我们永远无法确切知晓,我们只能依据我们的观察,尽量对X的数值进行估算。
X的左侧新增了一个带有上标的减号,这表明该数值是基于前一时刻的状况进行推算得出的。稍后,我们将依据观测数据对其进行调整。经过修正后的X值,方为最精确的预估,即去除了上标减号的X。
凭借状态预测的公式,我们能够对此刻的状态进行推断;然而,我们清楚,每一次的推断都不可避免地掺杂了噪声。噪声程度越高,所伴随的不确定性也就越强。为了量化这种不确定性,我们便需要借助协方差矩阵来进行表达。
那么什么是协方差矩阵呢?我们还是从一维的简单情况来解释,
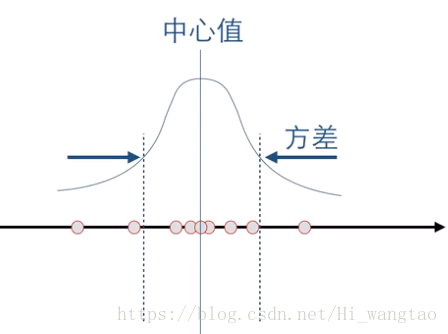
我们面对的是一维的含有杂音的数据集,其中每一次的测量结果均不相同,但它们都集中在某个中心点附近。为了描述这种数据的分布情况,最直接的方法是记录其中心值和离散程度,这背后隐含的假设是数据遵循高斯分布。
那么,让我们来探讨二维空间中的情形,观察那些混入噪声的二维数据,其呈现出的形态是这样的。
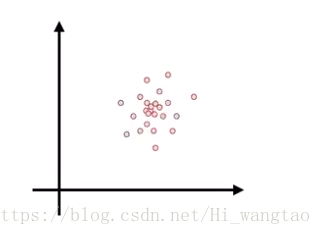
对这两个坐标轴各自进行投影后,若在各自轴向上均呈现高斯分布形态,那么在描述这一分布特征时,我们是否只需分别记录下这两个高斯分布的中心位置和各自的方差即可?
当两个维度的噪声相互独立时,我们能够以这种方式进行表达;然而,若这两个维度之间存在关联性,例如在一个维度上噪声增大的同时,另一个维度的噪声亦随之增大,那么这个图形将呈现出这样的形态。
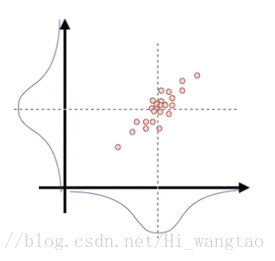
如果一个维度增大的时候,另一个维度减小,就会变成这样。
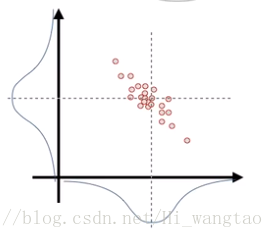
此时在两个坐标轴上的映射与首个映射毫无差异,依旧呈现高斯分布形态。因此,为了体现这两个维度间的关联度,我们不仅需记录各自的方差,还需引入协方差来衡量它们之间的相互关系。将它们以矩阵形式呈现,便是如此。
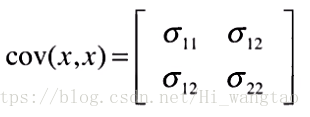
对角线位置上的数值代表了两个不同维度的方差值。而非对角线上的数值则彼此相等,这些数值代表的是协方差。在这三种情形下,左侧的斜方差值为零;居中的协方差值为正;而右侧的数值则显示出负相关性,其协方差值为负。在卡尔曼滤波器的应用中,涉及不确定性的所有描述都必须依赖于这个协方差矩阵。
以我们的小汽车为例,每个时刻的状态不确定性均由协方差矩阵P来具体体现。
接下来,我们要探讨的焦点是如何确保这种不确定性能够在各个时刻间得以传递?实际上,解决之道在于对状态转换矩阵F进行乘法运算。
这次操作需在两侧分别执行一次,左侧进行F的乘法运算,右侧则是对F进行转制处理,具体操作方法如下。
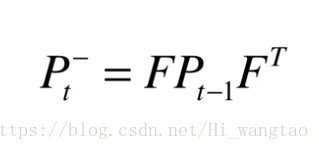
由前一次观测及当前估计的协方差,等同于前一个时刻的协方差两侧,与状态转移矩阵相乘。至于为何要乘以两侧,这体现了协方差矩阵的一个特性。X的协方差记作P,若要计算F与X协方差之积,可将F提出至等式两侧。
在这个阶段云开·全站体育app登录,我们必须注意到一个关键点,即我们的预测模型并非完全无误,它自身也存在着一定的误差,即噪声。因此,在后续步骤中,我们需要引入一个协方差矩阵q,以此来表征由预测模型自身引入的这种噪声效应。
好的,这个公式正是卡尔曼滤波器的第二公式,它揭示了不确定性在各个不同时间点之间是如何相互传递的。
以我们的小型汽车模型为例,若在公路的起始点安装一台激光测距设备,我们便能在任意时刻准确捕捉到汽车的具体位置。
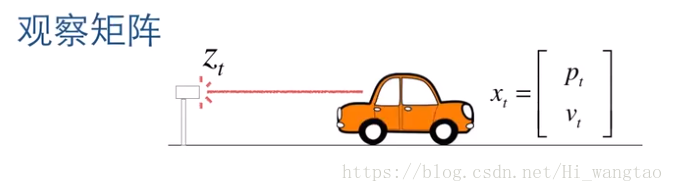
所观测到的数值被称作Z(t),而汽车本身的状态X(t)转变为观测状态Z(t)的过程中,存在一个转换关系,我们将其标记为H。显然,这种转换关系必须是线性的,因为卡尔曼滤波器本质上是一种线性滤波器。因此,我们自然地将H表示为矩阵形式,即所谓的观测矩阵。需要注意的是,X和Z的维度并不一定相等。
在本例中,X代表一个二维的列向量,而Z仅是一个单一的标量数值,因此H理应构成一个由一列和两行组成的矩阵,其内部的元素分别取值为一和零。
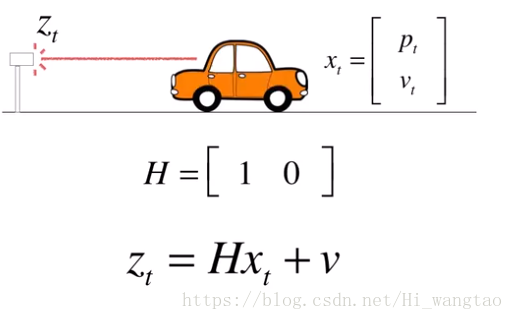
当h与x相乘时,便会生成一个标量结果Z。这个Z代表了汽车的具体位置,且与X的第一个数值相同。那么,为何还要额外加上一个小写的v呢?
观测数据并非完全准确,因此我们在后续分析中需引入V来表征观测误差,同时,该误差的协方差结构以R来表示。鉴于本例中观测数据为一维数值,故R的具体形式并非矩阵,而是一个单独的数值,专用于表示Z的方差。
若我们拥有除激光测距仪以外的其他测量手段来探测汽车的一项特性,那么Z将不再是一个单一的列向量,而是转变为一个包含多种测量手段所得数据的多元列向量。每个测量数值仅是对实际状况的一种片面反映,我们能够依据这些不全面的描述来推测出真实情况,而卡尔曼滤波器在数据融合方面的作用,则恰好体现在这个测量矩阵之中。
我们已掌握Z及其噪声的协方差矩阵R,接下来应如何将它们融入我们对状态的评估过程?
在前面的步骤中,我们已经成功求得了带有上标减号的X(t)开yun体育app官网网页登录入口,接下来,我们只需在原式基础上添加一个修正项,便能够得到我们追求的最佳估值。那么,这个需要添加的修正项究竟是什么呢?
观察括号内的内容kaiyun全站网页版登录,Z(t)减去H乘以X(t)的负指数,这一差值代表实际观测值与预期观测值之间的偏差。此偏差若乘以系数K,便能够对X(t)的数值进行校正。K系数至关重要,被称为卡尔曼系数。实际上,它也是一个矩阵,其计算公式如下。
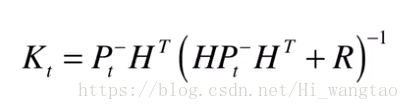
该公式的演算过程相对繁杂,因此我们仅对其性质进行探讨;卡尔曼系数K的功能主要体现在两个方面,分别是:
首先,需评估预测状态协方差P与观察量协方差矩阵R的规模,以确定对预测模型与观察模型的信任程度;其次,若更信任预测模型,则残差权重将相对较小;反之,若更信任观察模型,则残差权重将相对较大。
第二个作用在于将残差的表现形式,从观察域转换至状态域。这究竟意味着什么呢?我们之前提到,观察值z值构成一个一维向量,而状态值则是一个二维向量。这两个向量所采用的单位,以及所描述的特征,甚至可能完全不同。那么,我们究竟如何能够用观察值的残差来更新状态值呢?实际上,这个卡面系数k正是为了解决这一问题而存在的。
在这个案例中,我们仅对汽车的位置进行了观察。然而,在K中,已融入了协方差矩阵P的详细数据。因此,它借助位置与速度这两个维度之间的关联性,从位置残差中推断出速度残差,并对状态X的两个维度进行同步调整。
好的,现在我们仅剩最后一步,即对最佳估计值的噪声分布进行更新,这个分布将为下一轮迭代提供参考。在这一过程中,状态的不确定性将逐渐降低;然而,在下一轮竞赛中,由于噪声的传递,这种不确定性将再次上升。卡尔曼滤波器正是在这种不确定性波动中,努力寻找一种平衡状态。
现在,我们已成功掌握了卡尔曼滤波器的全部五个公式,不妨将它们逐一完整地展示出来,一睹为快。
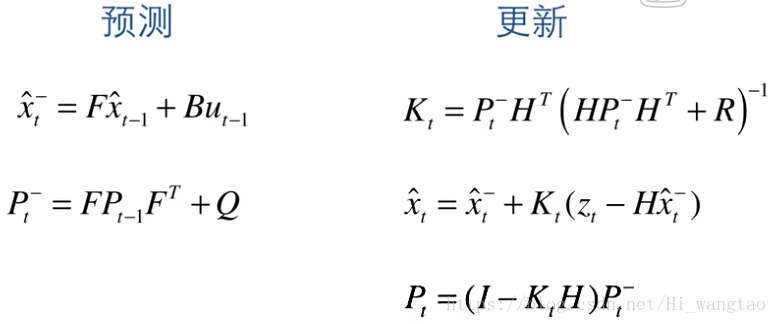
前两个公式是基于前一时刻的状态来推断当前时刻的状态,运用这两个公式,我们得到的是带有负号上标的X和P,这表明这并非最精确的估计。负号上标暗示着它们尚有不足之处。这种不足之处,正是观测诊断所提供的信息缺失,毕竟我们尚未将当前时刻的观测数据纳入考量。
那三个公式啊,主要是基于当前的观测数据来对X和P进行更新,更新后的数值即为最理想的观测数据,因此它们并不带有负号上标。
这是一段他人的视频内容,其讲解非常清晰易懂,令人印象深刻,因此我将其转化为文字,以便与大家共享。
好东西不能独享,是这样吗?哈哈。。。。。






