在Matlab中,DCT的计算有两种方法
(1) 使用基于FFT的加速方法的dct2函数
(2) dctmtc函数使用DCT变换矩阵
这里小编只重点演示(2)dctmtc函数的应用。第一个比较容易理解。
%%如果是三维图像(如RGB),必须先将图像转换为灰度图像或者使用reshape函数转换维度。
G=imread('F:\1\12636289.jpg');
数字
次要情节(121)
即时显示(G);
title('RGB原图');
W=rgb2gray(G);%rgb转灰度
W=im2double(W);%双精度类
次要情节(122);
即时显示(W);
title('双灰度');

T=dctmtx(8);%生成DCT变换矩阵
% x 每个分为8*8块,P1*x*P2相当于像素块的处理函数,p1=T p2=T',即fun=p1*x*p2'=T*x * T'的作用是进行离散余弦变换
Y = blkproc(W,[8 8],'P1 * x * P2',T,T'); %计算二维DCT
%P1*x*P2相当于像素块的处理函数
%,p1=T p2=T',进行离散余弦变换其中T为dctmtx(n)函数得到的DCT变换矩阵
掩码1 = [1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];
掩码2=[1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0];%保留10
掩码3=[1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 0
1 1 1 1 1 0 0 0
1 1 1 1 0 0 0 0
1 1 1 0 0 0 0 0
1 1 0 0 0 0 0 0
1 0 0 0 0 0 0 0];%保留36
掩码4=[ 1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留全部
掩码5=[ 0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留右下64-3
掩码6=[ 0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1
0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1];%保留右下64-10
掩码7=[ 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1
0 0 0 0 0 0 1 1
0 0 0 0 0 1 1 1
0 0 0 0 1 1 1 1
0 0 0 1 1 1 1 1
0 0 1 1 1 1 1 1
0 1 1 1 1 1 1 1];%保留右下64-36
%二进制掩码,用于压缩DCT系数
% 函数:blkproc
% 功能:图像的块处理
% 函数调用形式:B = blkproc(A,[mn],fun,parameter1,parameter2,...)
% B = blkproc(A,[mn],[mborder nborder],fun,...)
% B = blkproc(A,'索引',...)
% 参数解释:[mn]:将图像分为m*n个单元,对图像进行处理(如8像素*8像素)
% 乐趣:应用该函数分别处理每个m*n块的像素。
%parameter1,parameter2:要传递给fun函数的参数
% mborder nborder:将每个m*n块上下扩展mborder单位kaiyun全站网页版登录,左右扩展nborder单位。扩展后的像素值为0,fun函数处理整个扩展块。
%这里:fun='P1*x*P2',fun的参数P1,P2,将T,T'传给fun的参数,即:P1=T,P2=T'。
%丢弃每个块中的高频系数,达到图像压缩的目的
Y1 = blkproc(Y,[8 8],'P1.*x',mask1);
%仅保留DCT的10个系数
Y2 = blkproc(Y,[8 8],'P1.*x',mask2);
Y3 = blkproc(Y,[8 8],'P1.*x',mask3);
Y4 = blkproc(Y,[8 8],'P1.*x',mask4);
Y5 = blkproc(Y,[8 8],'P1.*x',mask5);
Y6 = blkproc(Y,[8 8],'P1.*x',mask6);
Y7 = blkproc(Y,[8 8],'P1.*x',mask7);
A1 = blkproc(Y1,[8 8],'P1*x*P2',T',T);%注意与上一个的区别
A2 = blkproc(Y2,[8 8],'P1*x*P2',T',T);
A3 = blkproc(Y3,[8 8],'P1*x*P2',T',T);
A4 = blkproc(Y4,[8 8],'P1*x*P2',T',T);
A5 = blkproc(Y5,[8 8],'P1*x*P2',T',T);
A6 = blkproc(Y6,[8 8],'P1*x*P2',T',T);
A7 = blkproc(Y7,[8 8],'P1*x*P2',T',T);
%%进行反余弦变换,得到压缩图像逆DCT开yun体育app官网网页登录入口云开·全站体育app登录,用于重建图像
图(2);子图(2,4,1),imshow(W),title('原图');
图(2);subplot(2,4,2),imshow(A1),title('压缩后重建图像6');
图(2);subplot(2,4,3),imshow(A2),title('压缩10后重建图像');
图(2);subplot(2,4,4),imshow(A3),title('压缩后重建图像36');
图(2);子图(2,4,5),imshow(A4),title('全部恢复');
图(2);subplot(2,4,6),imshow(A5),title('压缩后重建图像63-3');
图(2);subplot(2,4,7),imshow(A6),title('压缩后重建图像63-10');
图(2);subplot(2,4,8),imshow(A7),title('压缩后重建图像63-36');
%%
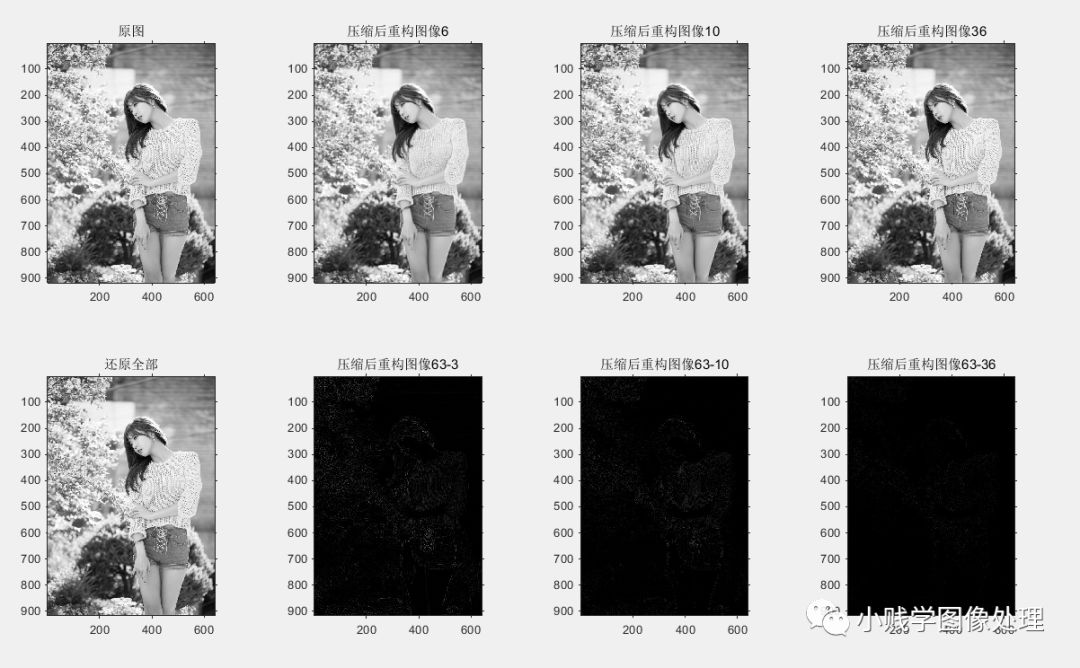
单独对比效果图
Y4 = blkproc(Y,[8 8],'P1.*x',mask4);%这是为了实验效果而添加的程序

Y1 = blkproc(Y,[8 8],'P1.*x',mask1);这里的mask1指的是左上角的6个1

Y2 = blkproc(Y,[8 8],'P1.*x',mask2);

Y3 = blkproc(Y,[8 8],'P1.*x',mask3);







