傅里叶:你可以知道信号中的分量,但对于非平稳过程,你无法看到每个分量出现的时刻。短时傅里叶变换-:固定窗口的傅里叶变换不能满足非平稳信号变化的要求。频率需求小波变换:时域能量有限,频域带通滤波1.傅里叶变换
1.1 原理
例子:
下图展示了对平稳信号进行傅里叶变换得到的频谱图的四个频域分量,分别是10Hz、25Hz、50Hz和100Hz。

为什么傅里叶变换可以得到信号的各个频率分量?
傅里叶变换使用一个无限长的三角函数作为基函数:这个基函数会拉伸和平移(其实它的本质不是平移,而是两个正交基的分解)。如果变窄,则对应高频;如果变窄,则对应高频;如果它被拉宽,则对应于低频。
然后,该基函数连续乘以信号。乘以某个尺度(宽度或窄度)的结果表示信号中包含的当前尺度对应的频率分量的数量。
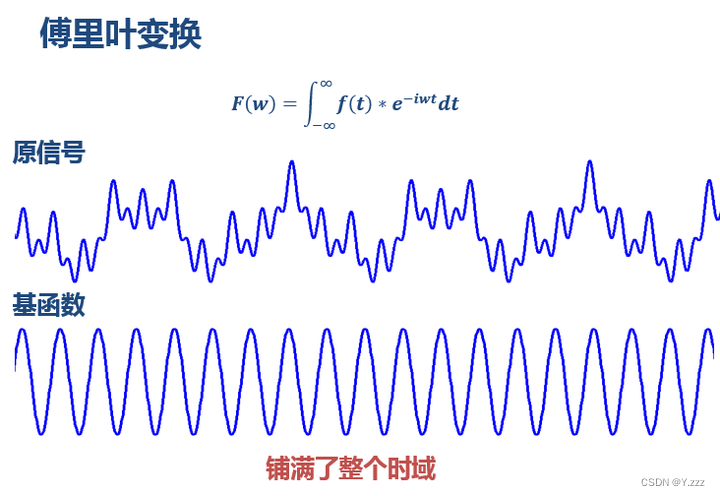
这一步实际上是计算信号与三角函数之间的相关性。在一定尺度下,基函数与信号相乘得到的值越大(相关性高),说明信号中包含的这两个频率成分越多,频谱上这两个频率处就会出现两个峰值。
1.2 缺陷
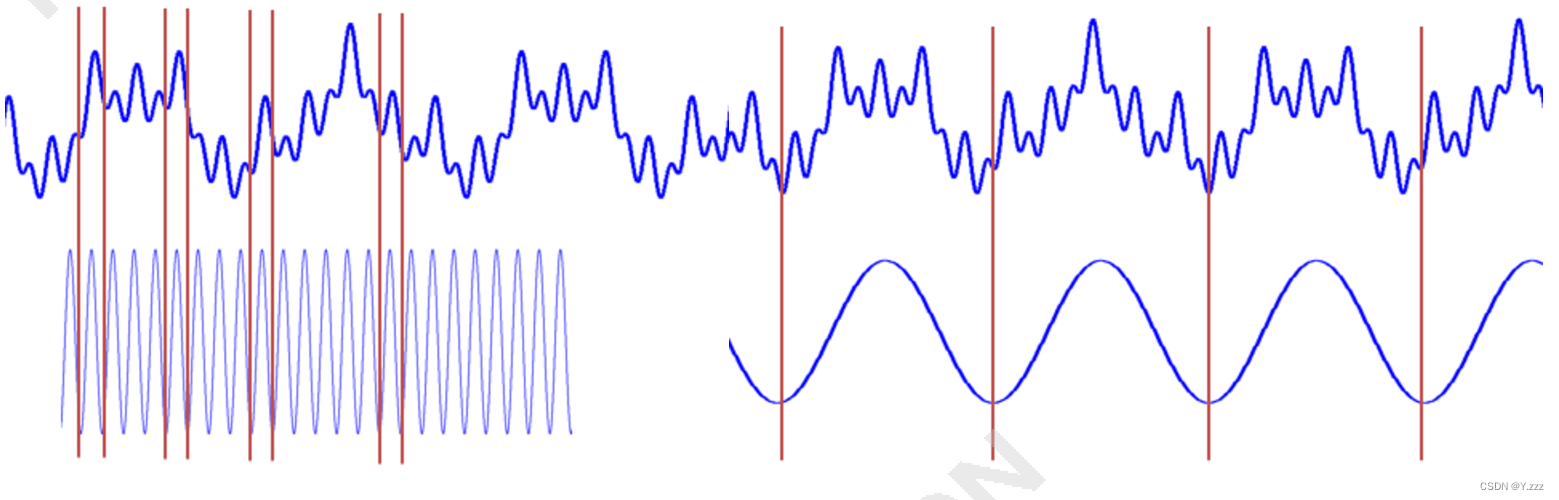
对平稳信号和频率随时间变化的非平稳信号进行FFT(快速傅里叶变换),如下图所示:
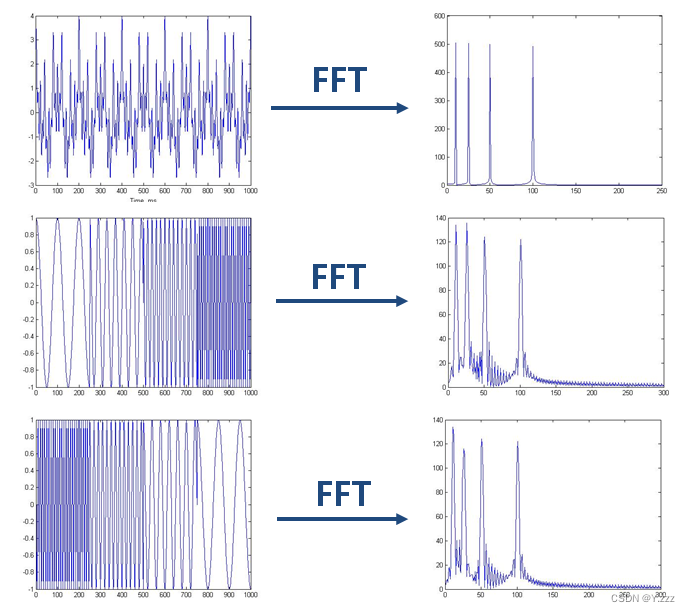
我们发现,这三个在时域上差异巨大的信号的频谱(幅度谱)非常一致。我们可以在频谱上看到四条清晰的线,这意味着所包含的四个频率分量是相同的,但它们出现的顺序不同。
可见,傅里叶变换在处理非平稳信号方面具有先天的缺陷。它只能获取一段信号一般包含哪些频率成分kaiyun.ccm,但不知道每个成分出现的时间。
2. 短时傅里叶变换(STFT) 2.1 概念
大多数平稳信号是人为产生的,自然界中大量信号几乎是非平稳的。对于这样的非平稳信号,仅仅知道它包含哪些频率分量是不够的。这也需要时频分析来了解每个分量出现的时间、信号频率如何随时间变化、每个时刻的瞬时频率及其幅度。一个简单可行的办法就是加窗户。
简单来说,短时傅里叶变换将整个时域过程分解为无数个等长、近似平稳的段,然后对每个段进行FFT(傅里叶变换),以确定频率分量随时间变化的频率分量。不断变化的情况。
对下图所示的非平稳信号进行短时傅里叶变换,得到该信号的时频图。时频分析结果如下图所示:不仅可以看到10Hz、25Hz、50Hz、100Hz四个频域分量,还可以看到出现的时间。 (两排峰是对称的,只看一排)
STFT变换后的时频图:
2.2 缺陷
使用STFT时,应该使用什么宽度的窗函数?
对于时变非平稳信号,高频适合小窗口,低频适合大窗口。
然而,STFT 窗口是固定的云开·全站体育app登录,宽度在 STFT 期间不会改变。
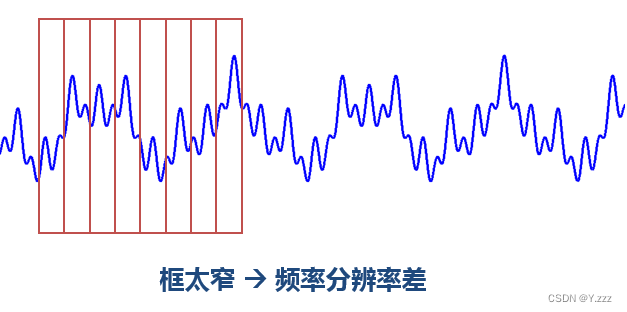
如果窗口太窄,窗口内的信号太短,则频率分析不准确,频率分辨率差;
窗口太宽,时域不够精确,时间分辨率低。
因此,STFT仍然无法满足非稳态信号变化的频率要求。
这是一对不可调和的矛盾。不存在绝对意义上的瞬时频率。我们只能知道在一段时间内存在某个频段的分量。
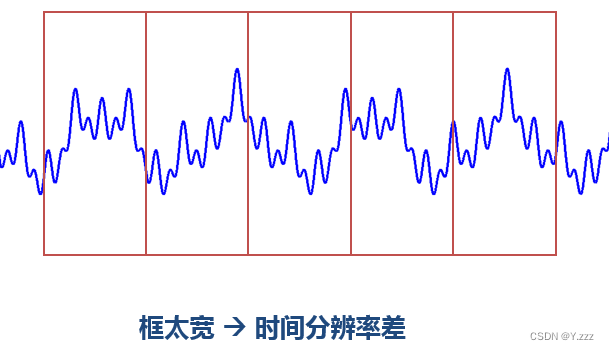
例子:
使用不同宽度的窗口对同一信号(4个频率分量)进行STFT,结果如右图所示。
窄窗口具有高时间分辨率和低频率分辨率。
宽窗口具有低时间分辨率和高频率分辨率。
由于窗口较窄,时频图在时间轴上的分辨率较高,且几个峰值基本呈矩形;
使用宽窗口时,时频图在时间线上变成了小山。
但频率轴上的窄窗口(1)显然不如下面的两个宽窗口(2)(3)准确;
(1) 用窄窗口进行STFT,结果如右图:
(2) 用宽窗口做STFT,结果如右图:
(3) 用宽窗口做STFT,结果如右图:
3.小波变换
傅里叶变换与傅里叶变换的区别短时傅立叶变换 |小波变换|:
差分傅里叶变换 短时傅里叶变换 小波变换
基函数
无限长三角函数基
无限长三角函数基
有限长度衰减小波基
图片
频谱,能够获取频率
频谱,能够获取频率
时间谱,可获取频率并定位时间
多变的
A、频率ω
A、频率ω
2、尺度a(scale)、平移量τ(translation)
窗户
添加固定窗口
误区:STFT给信号加一个窗口,分段进行FFT;小波变换没有使用窗的思想,也不进行傅里叶变换。不能认为小波变换只是添加不等长的窗口,改变窗口大小kaiyun全站网页版登录,对每个小部分进行傅里叶变换。
为什么叫“小波”?因为是很小的波浪~
从公式中我们可以看出,小波变换的变量包括尺度a(scale)和平移量τ(translation)。尺度a控制小波函数的膨胀和收缩,平移量τ控制小波函数的平移。尺度对应于频率(成反比),平移量τ对应于时间。
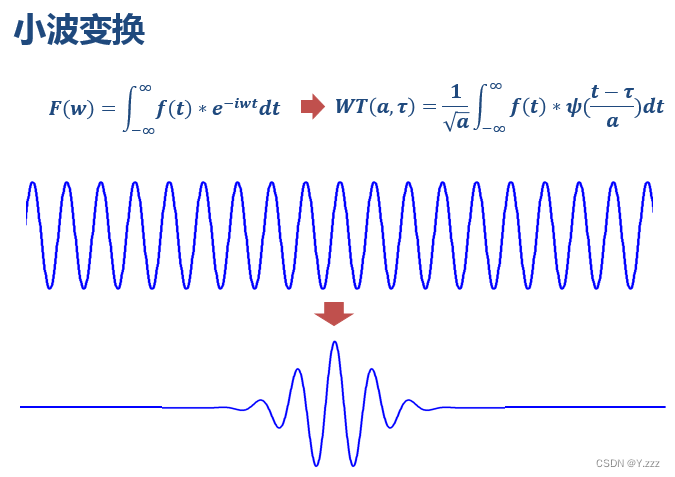
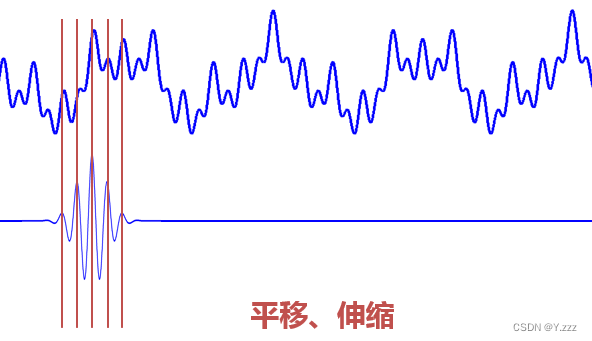
当缩放和平移到这种重合情况时,它们也会相乘以获得一个大值。与傅里叶变换不同的是,此时我们不仅可以知道信号有这样的频率成分,还可以知道它在时域中的具体位置。当我们在每个尺度上转换和乘以信号时,我们知道信号在每个位置包含哪些频率分量。
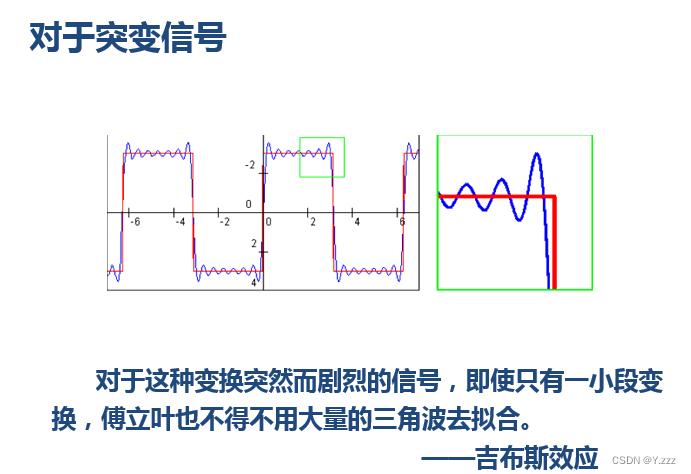
另外,对于突变信号,傅里叶变换存在吉布斯效应,我们无法用无限长的三角函数很好地拟合突变信号:
衰减小波:
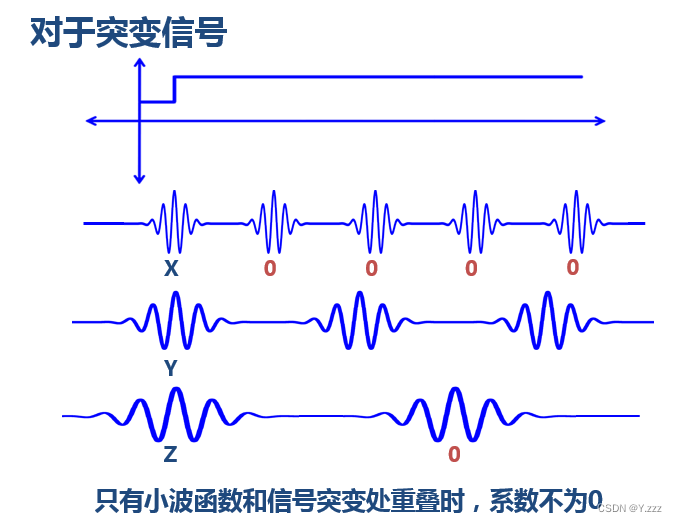
图片链接:THE WAVELET TUTORIAL(下载:THE WAVELET TUTORIAL)
参考原文链接:






