介绍
如果要正确理解小波变换,首先必须理解傅里叶变换。本文作者按照傅里叶-短时傅里叶变换-小波变换的顺序由浅入深地讲解了小波变换的原因和思想。帮助初学者深入了解傅里叶变换和小波变换。
从傅里叶变换到小波变换,并不是一个完全抽象的东西,可以描述得非常形象。小波变换具有明确的物理意义。如果我们看看它提出时所面临的问题,我们就能理出一个非常清晰的思路。
接下来我就按照傅里叶-->短时傅里叶变换-->小波变换的顺序来谈谈小波为什么会出现以及小波到底是什么。 (反正题问的是热门图片,并没有说要简短,希望不要太长,我就不看了。)
1. 傅里叶变换
这里我不再详细介绍傅里叶变换的基本概念。我假设每个人现在都在理解傅立叶的道路上,但尚未理解小波。 (在第三节讲小波变换时,我会形象地讲一下傅里叶变换)
下面我们主要讲一下傅里叶变换的缺点。也就是我们知道傅里叶变换可以分析信号的频谱,那为什么还要提出小波变换呢?答案就是@方沁源所说的“对于非平稳过程,傅里叶变换有局限性”。考虑以下简单信号:

进行FFT(快速傅里叶变换)后,您可以在频谱上看到四条清晰的线条,并且信号包含四个频率分量。
一切都很好。但如果它是频率随时间变化的非平稳信号呢?
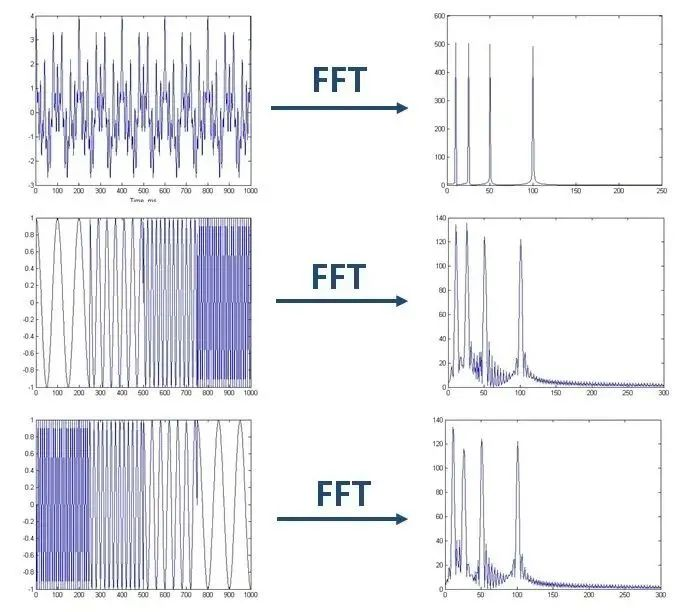
如上图所示,最上面的一个是频率恒定的平稳信号。较低的两个是频率随时间变化的非平稳信号。它们还包含四个与上部信号频率相同的分量。
经过FFT后,我们发现这三个时域差异巨大的信号的频谱(幅度谱)非常一致。尤其是下面的两个非平稳信号,我们无法从频谱上区分它们,因为它们所包含的四个频率信号的分量确实是相同的,只是它们出现的顺序不同。
可见,傅里叶变换在处理非平稳信号方面具有先天的缺陷。它只能获取信号一般包含哪些频率成分,但不知道每个成分出现的时间。因此,时域差异很大的两个信号可能具有相同的频谱。
然而,平稳信号大多是人为产生的,自然界中大量信号几乎是非平稳的。因此,在生物医学信号分析等领域的论文中,基本看不到简单傅里叶变换等朴素的方法。
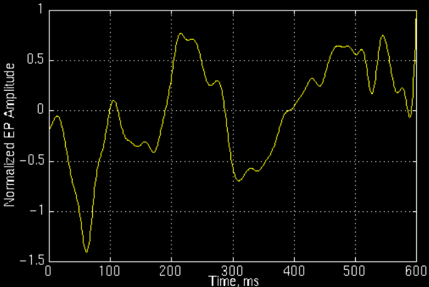
上图是正常人的事件相关电位。对于这样的非平稳信号,仅仅知道它包含哪些频率分量是不够的。我们还想知道每个组件何时出现。知道信号频率如何随时间变化,每一时刻的瞬时频率及其幅度——这就是时频分析。
2. 短时傅里叶变换(STFT)
一个简单可行的办法就是加窗户。我再用一下方沁源的描述,“把整个时域过程分解成无数个长度相等的小过程,每个小过程近似平稳。经过傅里叶变换,你可以知道事件发生在哪个时间点,发生的频率是多少?” “这就是短时傅里叶变换。
看图片:
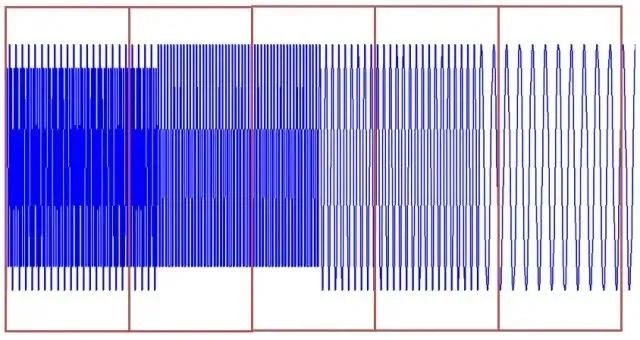
如果你把时域分成一段,做FFT,你不知道频率成分是如何随时间变化的吗?
利用这种方法,可以得到信号的时频图:
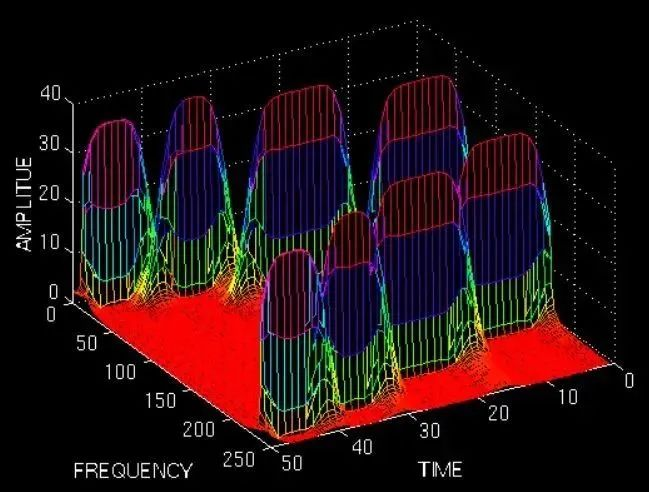
——此图来自《THE WAVELET TUTORIAL》
图中可以看到10Hz、25Hz、50Hz、100Hz四个频域分量,也可以看到出现的时间。两排峰是对称的,因此您只需看一排即可。
不是很好吗?时频分析结果可用。但STFT仍然存在缺陷。
使用STFT时有一个问题,我们应该使用多宽的窗函数?
窗户太宽或太窄会出现问题:
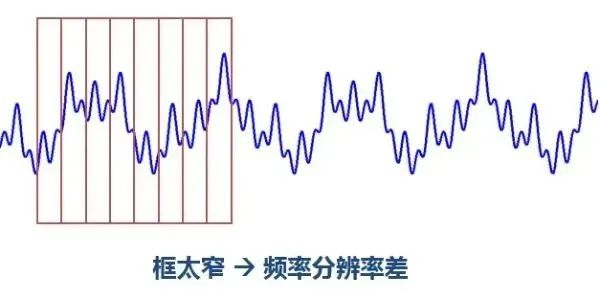

如果窗口太窄,窗口内的信号太短,则频率分析不准确,频率分辨率差。窗口太宽,时域不够精确,时间分辨率低。
(这里插一句,这个原理可以用海森堡测不准原理来解释。类似于我们无法同时获得粒子的动量和位置,我们也无法获得绝对准确的信号在的时间和频率同时这也是一对不能同时存在的矛盾,我们不知道某个时刻存在哪个频率分量,所以只能知道某个时间段内存在某个频段的分量。绝对意义上的瞬时频率并不 存在。)
看一下示例效果:
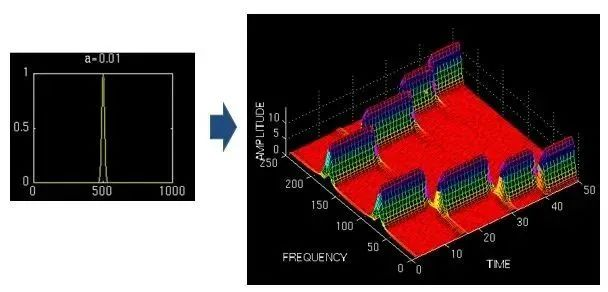
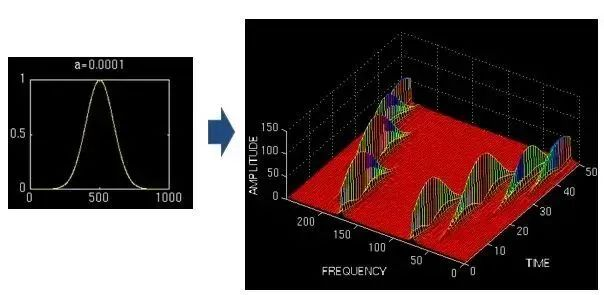
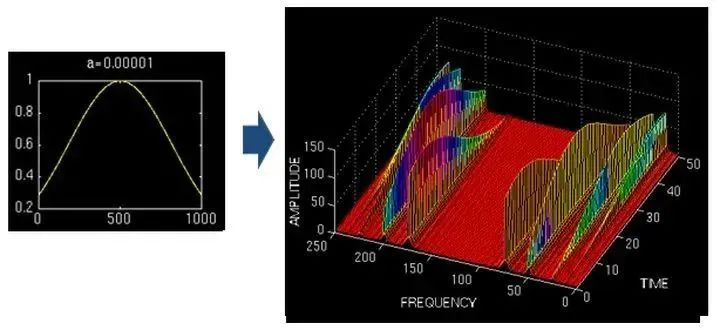
——此图来自《THE WAVELET TUTORIAL》
上图使用不同宽度的窗口对同一信号(4个频率分量)进行STFT,结果如右图所示。窗口窄时,时频图在时间轴上的分辨率非常高,几个峰基本呈矩形,窗口宽时,则变成长长的低山。然而,在频率轴上,窄窗口显然不如下面的两个宽窗口准确。
因此,窄窗口时间分辨率高,频率分辨率低,宽窗口时间分辨率低,频率分辨率高。对于时变非平稳信号,高频适合小窗口,低频适合大窗口。然而,STFT的窗口是固定的,一个STFT的宽度不会发生变化,因此STFT仍然无法满足非稳态信号变化的频率要求。
3.小波变换
那么你可能会想,改变窗口大小,多做几次STFT不就够了吗? !是的,小波变换就有这个思想。
但事实上,小波并没有这么做(关于这一点,方沁源所说的“小波变换是在算法的基础上,加入不等长的窗口,对每个小部分进行傅里叶变换”的说法是不准确的。小波变换没有使用windows的思想,也不进行傅里叶变换)。
至于为什么不使用可变窗口的STFT,我认为是因为冗余太严重了。 STFT不能正交化,这也是它的一大缺陷。
因此,小波变换的出发点与STFT还是不同的。 STFT给信号加窗并分段进行FFT;而小波则直接改变了傅里叶变换的基础——用有限长度的衰减小波基代替了无限长的三角函数基。这样不仅可以获取频率,还可以定位时间~
【解释】
让我们再次回顾一下傅里叶变换。不明白为什么傅里叶变换可以得到信号各个频率分量的同学也可以用我的图来理解。
傅里叶变换使用无限长的三角函数作为基函数:
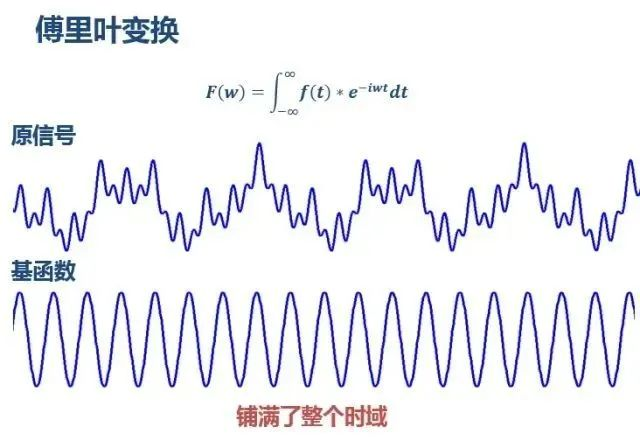
这个基函数会拉伸和平移(其实它的本质不是平移,而是两个正交基的分解)。如果变窄,则对应高频;如果变窄,则对应高频;如果它被拉宽,则对应于低频。然后这个基函数连续乘以信号。乘以某个尺度(宽度或窄度)的结果可以理解为信号中包含的当前尺度对应的频率分量的数量。因此,基函数会与信号相乘,得到一定尺度下的较大值,因为此时两者存在重叠关系。然后我们就知道信号包含多少该频率。
如果你仔细看的话,你可以发现这一步实际上是在计算信号和三角函数之间的相关性。
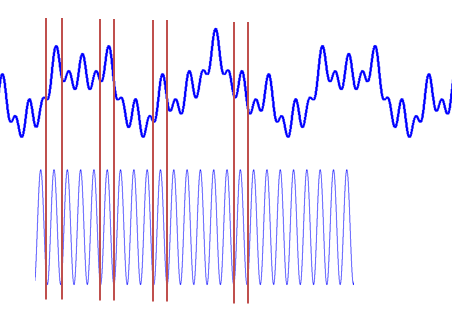
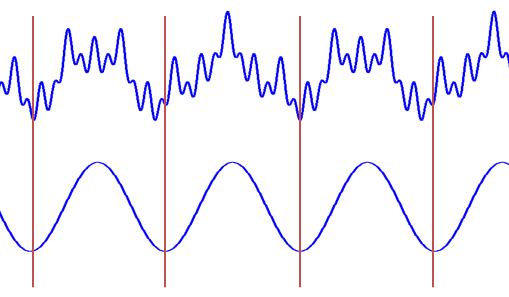
看,这两个尺度可以相乘到一个很大的值(高相关性),因此信号包含更多的这两个频率分量,并且频谱上这两个频率处会有两个峰值。
以上是粗浅意义上的傅里叶变换原理。
如前所述,小波所做的改变就是用有限长度的衰减小波基代替无限长度的三角函数基。
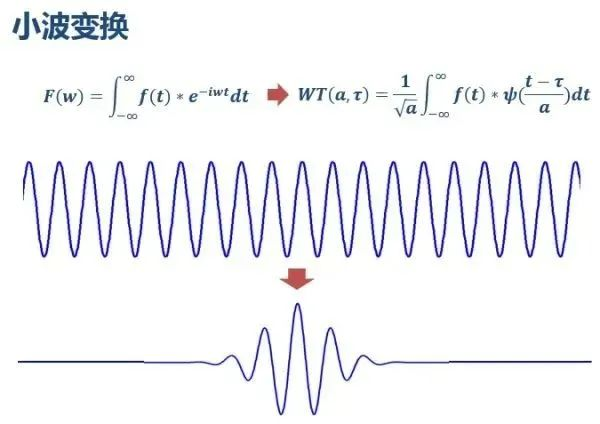
这就是为什么它被称为“小波”,因为它是一个非常小的波~
从公式中可以看出,与傅里叶变换只有频率ω作为变量不同,小波变换有两个变量:尺度a(scale)和平移量τ(translation)。尺度a控制小波函数的膨胀和收缩,平移量τ控制小波函数的平移。尺度对应于频率(成反比),平移量τ对应于时间。
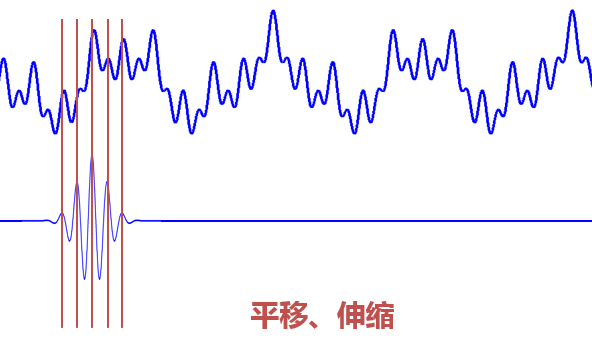
当缩放和平移到这种重合情况时,它们也会相乘以获得一个大值。此时与傅里叶变换不同的是,我们不仅可以知道信号有这样的频率成分,而且还可以知道它在时域中的具体位置。
当我们在每个尺度上转换和乘以信号时,我们知道信号在每个位置包含哪些频率分量。
你看到了吗?有了小波,我们不再害怕不稳定的信号!从现在开始你就可以进行时频分析了!
你只能通过傅里叶变换得到频谱,但通过小波变换你可以得到时间频谱!

↑:时域信号

↑:傅里叶变换结果
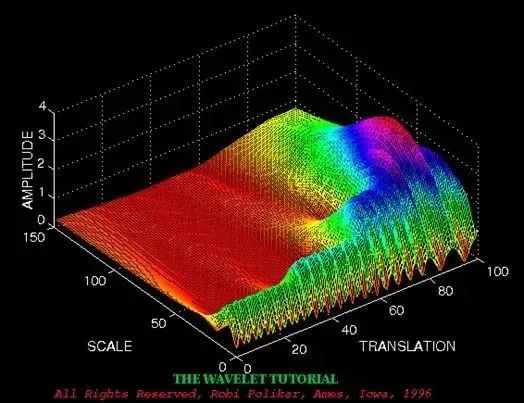
——此图来自《THE WAVELET TUTORIAL》
↑:小波变换结果
小波也有一些好处。例如,我们知道对于突变信号,傅里叶变换具有吉布斯效应,我们无法使用无限长的三角函数很好地拟合突变信号:
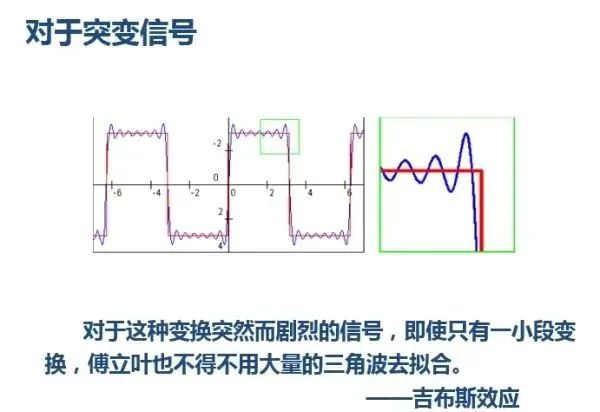
然而kaiyun全站网页版登录,衰减小波则不同:
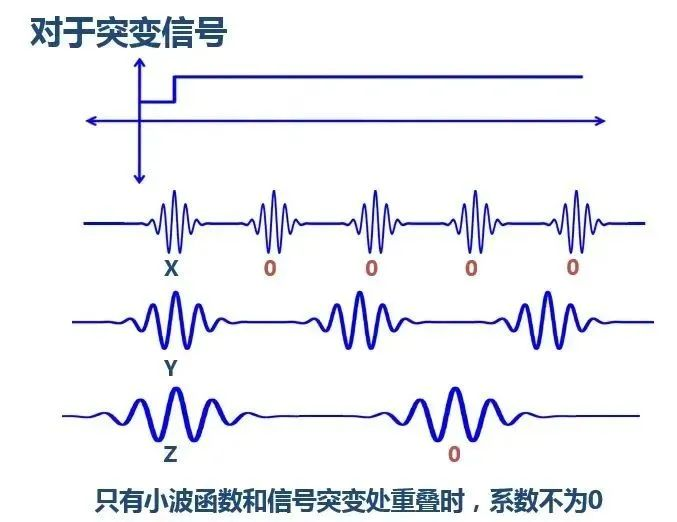
以上就是小波的含义。
-------------------------------------------------- -------------------------------------------------- --------
以上只是一个形象的向大家展示小波的思想。希望能给大家的入门带来一些帮助。毕竟,如果你对小波一无所知,直接去看那些堆公式、照搬论文语言的教科书肯定会很痛苦。
这里推荐几本入门读物,主要是感性介绍。它们很容易理解,但并不深入。它们对于大家初步了解小波会有很大的帮助。文章中的一些想法和图片也选自其中:
1. 小波教程(强烈推荐,点击链接:I~polikar/WTtutorial.html)
2. 小波:见森林、见树木
3. 非常友好的小波指南
4. 概念小波
但要真正理解透明小波变换还有很长的路要走。例如,你至少要知道有一个“尺度函数”,它是构造“小波函数”的关键,它和小波函数一起构成了小波多分辨率分析。只有了解了它,才有可能利用小波来做一些数字信号处理;还需要了解离散小波变换、正交小波变换、二维小波变换、小波包……这些内容国内教材也教得不好,就一点点看吧~
------
一些问题的回答:
1.关于海森堡测不准原理
测不准原理,或者说测不准原理,最早来自量子力学,指的是在微观世界中,粒子的位置和动量无法同时确定。但这一原理并不局限于量子力学。许多物理量都具有这样的特性,例如能量和时间、角动量和角度。它体现在时域和频域的信号场中。但更准确的说法应该是:一个信号不能同时过于集中在时空域和频域;函数在时域中越“窄”kaiyun.ccm,经过傅里叶变换后在频域中的函数就越“宽”。
如果你有兴趣深入研究的话,这个原理其实很耐人寻味。信号处理中的一些新理论也与它有根本的联系,例如压缩感知。如果剥开它复杂的数学描述,你最终会发现它的本质与不确定性原理密切相关。你不觉得这样矛盾的事情在哲学意义上也很美妙吗?
2. 关于正交化
什么是正交化?为什么小波可以实现正交化是一个优点?
简单地说,如果使用正交基,变换域系数将没有冗余信息,变换前后的信号能量相等,这意味着用最少的数据表达最大的信息量,有利于数值压缩等领域。 JPEG2000 压缩使用正交小波变换。
例如,二维笛卡尔坐标系的典型正交基:(1,0)、(0,1)。用它们来表达信号显然是非常高效的,而且计算也很简单。如果用三个互成120°的向量来表达,就会出现信息冗余和重复表达。
但这并不意味着正交性一定优于非正交性。例如,如果你在做图像增强,有时你希望有一些冗余信息,这样更有利于噪声抑制和某些特征的增强。
3.关于瞬时频率
原题:图中的时间点对应一个频率值。某一时间点只有一个信号值。我们怎样才能得到它的频率呢?
非常好的问题。正如文章中提到的,绝对意义上的瞬时频率实际上并不存在。如果你只看某个时间点的信号值,当然无法得到它的频率。我们只是用一小段信号的频率作为该时刻的频率,所以我们得到的只是一个时间分辨率有限的近似分析结果。这个想法在 STFT 中很明显。小波利用衰减基函数来测量信号的瞬时频率,其思想类似。 (不过说到希尔伯特变换,思路就不一样了,后面有机会我会详细解释)
4.关于小波变换的缺点
这取决于你与谁比较。
A、作为图像处理方法开yun体育app官网网页登录入口,与多尺度几何分析方法(超小波)相比:
对于图像等二维信号,只能在两个方向上进行二维小波变换。图像中点的信息表达还可以,但线条对齐性比较差。图像中最重要的信息正是那些边缘线。这时脊波(ridgelet)、曲线波(curvelet)等多尺度几何分析方法就更有优势了。
B、作为时频分析方法,与希尔伯特黄变换(HHT)相比:
与HHT等时频分析方法相比,小波仍然没有摆脱海森堡测不准原理的约束。在一定规模下,时间和频率不能同时具有高精度;而小波是非自适应的,基本上一旦选择了函数,就不会改变。
五、关于文章表达的严谨性
很多朋友在评论中提到我的一些说法不够准确。这是肯定的,我知道。比如在傅里叶变换的理解部分,我说的“乘一个大值”的表达肯定是不够严谨的。我也在评论中解释了细节。我想说的是,易懂性和精确性是很难兼顾的。如果想追求严谨,最好的就是课本上的数学表达式。它们是无可挑剔的,但对于初学者来说,可能有一个门槛。如果想用通俗的方式来解释,必然只关注一个关键点,就会出现漏洞。我想这就是教科书从来不写下这些通俗解释的原因——不是作者不懂,而是怕犯错误。因此,想要深入了解傅里叶变换和小波变换的朋友也应该仔细研读教材。如果这篇文章能给一些初学者一点帮助,我就很满足了。







