了解离散的傅立叶变换(IV)
----------------------------------------------------------------------------- ----------------------------------------------------------------------------- -----------------------------------------
复杂形式中离散的傅立叶变换非常巧妙地使用了复杂方法,从而使傅立叶变换更加自然和简洁。它不仅使用替代方法使用复数数字,而且还从复数的角度完全分析了问题。一件事与Real DFT完全不同。
1。表示余弦函数作为复杂形式
Euler方程可用于表示正弦余弦函数作为复杂形式:
cos(x)= 1/2 EJ(-X) + 1/2 EJX
sin(x)= J(1/2 EJ(-X)-1/2 EJX)
从这个方程式,我们可以看到,如果正余弦函数表示为复杂数,它们将成为由正频率和负频率组成的正余弦波。相反,由正频率和负频率组成的正余弦波可以通过复数形式来表达。
我们知道,在实际的傅立叶变换中,其频谱为0〜π(0〜n/2),但不能表示-π〜0的频谱。可以预见的是,如果正余弦表示为复杂形式,则可以包括负频率。
2。将转换之前和之后的变量视为复杂形式
傅立叶变换将原始信号x [n]视为由复数代表的信号,其中实际零件代表原始信号值,虚构部分为0,而转换结果x [k]也是一种复杂形式,也是一个复杂形式,但是,这里的零件值是重视的。在这里,我们应该从复数的角度看原始信号,这是理解复杂形式傅立叶变换的关键(如果您学习了复杂的变量函数,则可以更好地理解,即将x [n]视为一个复杂的变量,然后将其视为该复杂变量与实数相同)。
3。对复数执行相关算法(正向傅立叶变换)
从实际的傅立叶变换中,我们可以知道我们可以以正交函数形式将原始信号乘以信号,然后计算总和,最后我们可以获得原始信号中包含的正交函数信号的组件。现在,我们的原始信号已成为一个复杂的数字,我们想要获得的当然是复数数字的信号组成部分。我们可以以复杂数字的形式将其乘以正交函数吗?答案是肯定的。余弦函数是所有正交函数。在成为以下形式的复杂数字之后,它仍然是一个正交函数(可以从正交函数的定义中很容易证明这一点):
cos x + j sin x,cos x - j sin x,…
在这里kaiyun.ccm,我们使用上面的第二个方程来总结相关性。为什么使用第二个方程式?稍后,我们将知道正弦函数被转换为假想数并获得负正弦函数。在这里,我们将添加一个负符号,以使最终结果是正弦波。基于此,我们可以轻松地以复杂形式获得DFT正向转换方程:
该公式可以轻松获得Euler转换公式:
实际上,为了表达表达,我们使用Euler Transformation。解决问题时,我们仍然更频繁地使用正弦余弦表达式。
对于上述方程式,我们需要清楚以下方面(以及与实际DFT有什么不同):
1。x[k]和x [n]是复数,但是x [n]的虚构部分由0组成,实际部分代表原始信号。
2。k的值范围为0〜n-1(也可以表示为0〜2π),其中0〜n/2(或0〜π)是正频率部分,N/2〜N-1( π〜2π)是负频率部分。由于正余函数的对称性,我们表示–π〜0为π〜2π,这是为了计算便利。
3。J是一个不可分割的组件,就像方程中的变量一样,它不能随便删除,含义在删除后将完全不同,但是我们知道在实际DFT中,J只是一个符号。删除J,整个方程式的含义保持不变;
4。下图是连续的信号频谱,但是离散频谱也相似,因此它不会影响我们对问题的分析:
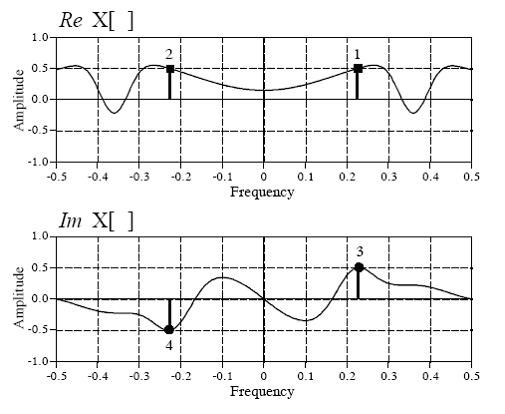
上面的频谱图将负频率放在左侧,以迎合我们的思维习惯,但是在实际实施中,我们通常将其移到正频谱后面。
从上图可以看出,根据先前一个等式中的一个比例系数为1/n(或1/2π),而不是2/n。这是因为现在频谱扩展到2π,但是在下面的描述中,可以更清楚地看到添加正频率和负频率2/n开yun体育app官网网页登录入口,然后恢复为真实DFT的形式。由于复杂的DFT生成了一个完整的频谱,因此原始信号中的每个点由两个频率组成,即正和负频率,因此频谱中每个点的带宽相同,并且是1/n。与真实的DFT相比,两端的带宽比其他点要少。
复杂DFT的频谱特性是周期性的:-n/2〜0与N/2〜N -1相同。实域频谱甚至是对称的(代表余弦波谱),而虚谱是奇怪的对称的(代表正弦波谱)。
4。反向傅立叶变换
假设我们已经获得了复杂的频谱x [k],现在我们需要将其还原到复杂的原始信号x [n],当然我们应该将x [k]乘以一个复杂的数字,然后将其汇总,然后将其汇总,最后获取原始信号x [n]。复数乘以x [k]首先使我们想起上述计算的复数:cos(2πkn/n) - j sin(2πkn/n),但在微小的负迹象中,实际上是为了使得正弦执行逆傅立叶变换时,功能成为一个正符号。由于虚构数字J的操作专长,应为正的正弦函数将成为负面的正弦函数(从后续的派生到这一点,我们将在此处看到),因此,减去符号只是为了纠正符号的功能。执行逆DFT时,我们可以删除负符号,因此我们获得了类似的DFT变换方程:
x [n] = x [k](cos(2πkn/n) + j sin(2πkn/n))
现在我们分析了这个方程式,我们会发现该方程实际上可以获得与实际数字的傅立叶变换相同的结果。让我们首先转换x [k]:
x [k] = re x [k] + j im x [k]
这样,我们可以再次转换x [n],例如:
x [n] =(re x [k] + j im x [k])(cos(2πkn/n) + j sin(2πkn/n))
=(re x [k] cos(2πkn/n) + j im x [k] cos(2πkn/n) +
j re x [k] sin(2πkn/n) - im x [k] sin(2πkn/n))
=(re x [k](cos(2πkn/n) + j sin(2πkn/n)) + --------------------------------(1)
im x [k](-sin(2πkn/n) + j cos(2πkn/n)))-------------------------------(2)
目前,我们将原始方程式分为两个部分。第一部分乘以真实域中的频谱,第二部分乘以虚拟域中的光谱。根据频谱图,我们可以知道re x [k]是一个均匀的对称变量,而im x [k]是一个奇数对称变量云开·全站体育app登录,即
re x [k] = re x [-k]
IM X [K] = -IM X [-K]
但是K的范围为0〜N-1、0〜N/2表示正频率,而N/2〜N-1表示负频率。为了方便表达,我们使用n/2〜n -1表示-k,因此在从0到n -1的求和过程中,有公式(1)和(2)的k和-k的总和,对于公式(1),有:
re x [k](cos(2πkn/n) + j sin(2πkn/n)) + re x [-k](cos(-2πkn/n) + j sin(-2πkn/n))
根据甚至对称和三角函数的属性,简化了上述公式以获得:
re x [k](cos(2πkn/n) + j sin(2πkn/n)) + re x [k](cos(2πkn/n)-j sin(2πkn/n))
该公式的最终结果是:
2 re x [k] cos(2πkn/n)
考虑到re x [k]方程中有比例系数1/n,将1/n乘以2,这是否与实际DFT中的方程相同?
对于公式(2),使用相同的方法,我们还可以得到以下结果:
-2 im x [k] sin(2πkn/n
请注意,上述方程式的前面有一个负符号,这是由虚构数字转换的特殊性引起的。当然,我们不能将负符号的正弦功能添加到余弦中。幸运的是,我们在上一个示例中使用了cos(2πkn/n)。 - j sin(2πkn/n)执行相关计算,结果是IM x [k]中的负符号,因此最终结果中正弦函数中没有负符号。这就是为什么在执行相关计算时,假想部分中使用负面迹象的原因(我认为这可能是复数DFT的美,这使人们感觉像是拼凑在一起的)。
从上面的分析中,我们可以看到,在执行反向变换时,通过实际傅立叶变换和复杂的傅立叶变换获得的结果是相同的,但是它们是不同的路径和相同的目的地。
附件:Word文档下载地址:






