大家好,我们再次见面。我是你的朋友Quanzhanjun。
我在论坛上看到一个朋友问为什么傅立叶变换可以将时域更改为频域?这个问题确实是灵魂的深处。
在这里,我只能简要谈论我的理解。深入了解,转动信号处理教科书是最好的方法。
1。如何描述信号我们经常使用数学模型来抽象物理事件。信号也可以通过数学模型表示。使用信号的数学模型,我们可以使用数学计算对信号模型进行各种更改。如果我们添加有关计算机,模拟和数字电力的相关知识,则可以将更改转换为信号模型的变化,以更改物理信号以实现我们的信号处理。如何使用数学模型描述信号?首先,肉眼可以看到的电磁波(光)与时间有关。因此,我们有一个时间域分析模型kaiyun.ccm,该模型非常直观并且与t相关。当放置在二维平面上时,轴之一是时轴。我们还使用振幅值作为第二轴来描述信号的强度。这是为了描述使用二维坐标的信号。应当指出的是,描述信号行为的目的是促进我们分析信号和数学过程,因此我们更喜欢单个变量的简单信号描述方法。当我们学习时,我们还开始从简单的单个变量信号中学习。
2。为什么要分析频域中的信号?对于某些具有时间变化模式的信号,例如定期信号,人们发现使用频率W描述它比使用时间t描述它更有效(为什么?W包含定期信息)。因此,有一种使用W轴描述信号而不使用T轴的方法,这是频域分析模型。如果您还不明白。然后,我只能通过从结果中推论原因来向您解释。
可以在时域中绘制如上图的信号,但是我们很难分析和处理信号。
从频域描述此信号时,我们发现我们看到了这样的常规图像。许多信号处理功能(例如过滤)可以在频域中如此轻松地实现。 (因为我们如此清楚地看到该信号的各种频率组件)因此,无论是时域还是频域,目的都是相似的,但是我们使用未使用的透视图来描述信号。信号处理开发后,人们逐渐发现只能在频域中处理某些信号。
3。打开时域和频域:傅立叶变换刚刚提到的两个域都可以描述一个物理事物,因此必须在这两个数学模型之间有一种相互转换的方法。我们的物理学家傅立叶提出了相互转化的方法,人们称之为傅立叶变换。傅立叶是如何提出傅立叶变换公式的?对于每个不同的信号,我们是否需要建立不同的公式?例如,两个声波信号“ Hello”和“ Hello”可以用两个公式描述。应该使用多少个公式来描述世界上这么多单词?我们解决此问题的想法是将标准公式归一化并使用不规则和多样化的信号组合在一起。因此,信号分解存在问题。就像化学定义一样,它将物质分解为具有统一特性的原子分子等。因此,有机化学可以合成各种高强度材料。傅立叶提出任何连续的周期信号都可以由多个正弦曲线组成。
从时域开始,正弦波和第三谐波(+)形成常规合成波。如果有更多的谐波,则方波将大约在周期。因此,他提出了这样的公式,f(t)代表了时域周期函数。
周期性的时域波形可以由正弦函数及其谐波添加组成。在
然后与这个很棒的公式合作
您可以将公式变成此
哇,这似乎非常接近我们经常看到的傅立叶变换公式。以上所有都是定期信号。对于非周期性信号g(t),我们可以将其视为具有无限周期性的周期性信号。因此,当t接近无限时,公式会重写。我得到了熟悉的傅立叶变换公式
此时,连接了时域和频域,并且可以将时域信号与频域正弦信号结合使用。随后的傅立叶变换的各种特征和属性为我们建立了一个宏伟的信号处理系统。在此系统上,我们建立了数字通信系统(通信),多媒体系统(终端)和AI(各种识别和交互)。
傅立叶变换概念和公式扣除
傅立叶变换的目的是将时域(即时域)中的信号转换为频域中的信号(即频域)。由于域是不同的,因此对同一事物的理解将相应地改变。 ,因此,在时间域中的某些难以处理的区域中,可以在频域中相对处理。
(w表示频率,t表示时间,e^-iwt是一个复杂的函数)傅立叶变换认为,周期函数(信号)包含多个频率组件,任何函数(信号)F(signal)f(t)可以通过多个周期性函数(基本功能)添加到合成。从物理的角度来看,傅立叶变换是基于一组特殊功能(三角函数)作为正交基础在原始函数上线性转换的。物理含义是在每组基础函数上的原始函数的投影。
我们首先将函数f(t)推断为周期函数,然后推断出非周期函数的傅立叶变换。傅立叶公式通常是指非周期性行函数的傅立叶变换(FT)。 (1)对于f(t)的函数,周期为1:
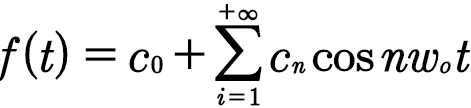
(我将在这里用t代表x)
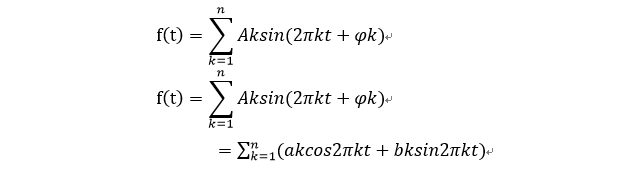
根据欧拉的公式
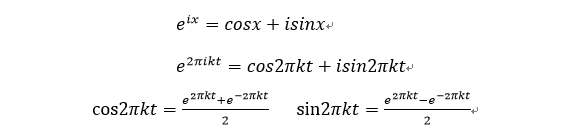
CK这是一个复杂的数字,CK通常称为傅立叶系数。频域的转换通常会改变CK。
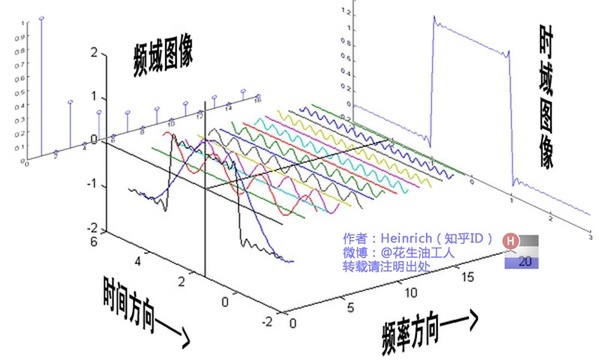
例如,在此图中,频域方向上的每个频域值是CK的值。
接下来,从
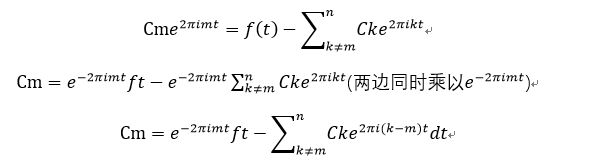
整合功能的两面
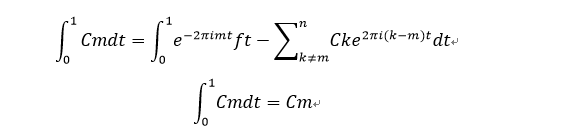
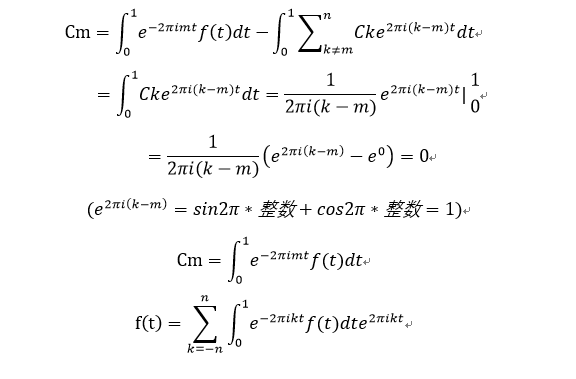
(以上k是指频域中的x坐标,每个k值是一个赫兹,t表示时间域中的时间),因为要模拟信号,无法通过添加有限的周期性函数来确定信号。有了很大的错误,我们无法获得完整的近似值,因此我们使用无限的周期性函数将其近似。
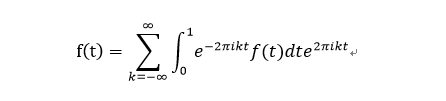
从中,我们可以看到傅立叶变换是时域和频域之间的变换关系。
(2)对于非周期性函数f(t),对于信号的处理,信号通常不是周期性的,因此在此生成非周期函数(信号)的处理。对于非周期性函数,我们可以假设非周期性函数是周期函数的一部分,但是该非周期函数的t范围可能很大。当该周期接近无限时,它是傅立叶系数中傅立叶系数的概括。反傅立叶变换是傅立叶序列的概括。假设F(t)是具有周期t和t接近无限周期函数的函数
傅立叶系列[F(t)]转换为
傅立叶系数为(注意:因为它在无限周期t下,所以从0-> t和(-t/2) - >(t/2)的数字相同)
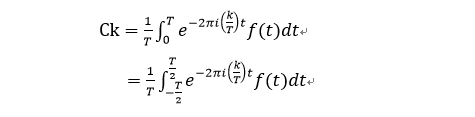
您在频谱图中看到的每条垂直线都是| ck |的值
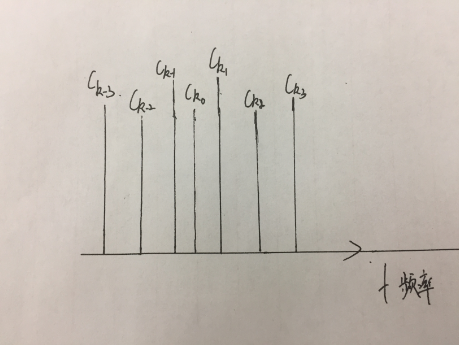
这是一个频谱图,其中时间域中的函数图像通过傅立叶变换进行了转换。对于具有周期1的函数,频域中每条线的间隔为1,对于具有周期t的函数,频域中的间隔为1/t,这一点非常重要。时间域周期与频域成反比。
也就是说,当t> 1-> 1/t尤其是当T接近无限时,频谱间隔越来越近,频谱最终变得连续时,T1/T> 1频谱将扩展。从中,我们可以得到一个普遍的说法:当域从周期性转变为非周期性时,频域将从离散转换为连续。看来您可以将非周期性功能视为周期性功能的一部分,以便可以产生傅立叶变换的结果?实际上,这不是完全正确的。因为当t接近无限CK时,趋于零,因此整个傅立叶系数的公式是毫无意义的:让f(t)为间隔A和B之间的0为0,请花大量时间t使A> -t/2 && b> T/2,然后用t作为函数扩展(| ck |是一个复杂的函数,因此对X轴是对称的),如下图所示:
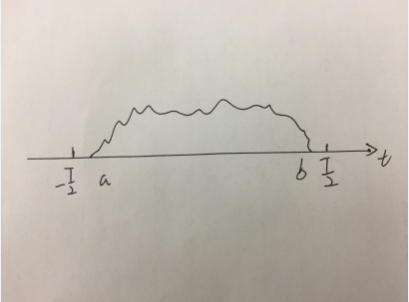
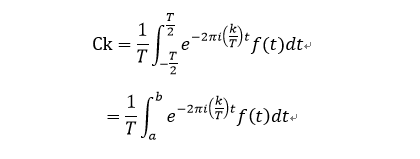
(A和B之外的功能为0)
(负数的值为1)
目前,此值是固定值m,即
也就是说,CK = 0。即使每个频率的系数为0,f(t)的用途是什么?为此,让我们从另一个角度开始GF成为有关K/T的功能:GF(K/T)
(即,CK不需要1/T的部分)
(此处得出f(t)的结果与上述相同),因为t->∞,gf(k/t)中的离散变量k/t越来越近,1/t,2/t,2/t,3 /t ...这样,函数从离散变为连续。我们将此K/T连续变量设置为S
关于f(t),f(t)可以被视为无数连续的gf(s)e^2πist,将其乘以1/t,以形成其作为积累和转化为积分。现在
这样,我们最终获得了傅立叶变换公式(ft)(傅立叶变换也可以称为操作员):
顺便说一句,给出傅立叶反变形公式:
文章参考:
这最初是我对Zhihu问题的回答,但实际上,这是我在数学和信号处理的本科研究中的想法。关于Zhihu的答案是急忙写的,只写了一些一般的想法而没有具体的发展。没有图片,很难理解。我在这里重组了它,并将其编译到本文中。
本文要求读者根据对傅立叶变换的一定理解,至少知道如何计算傅立叶变换。此外,有些地方要求读者为微分方程有一定的基础,至少他们可以找到简单谐波振荡器的二阶普通微分方程。
什么是傅立叶变换
在高级数学中,通常是从一系列周期函数中引入的,这也不例外。简而言之,我们从高中了解到,可以通过三角功能来描述理想的浪潮,但实际上,波浪可能具有各种奇怪的形状。首先,让我们看一下固定时期的波浪。下图显示了4个常见周期波。傅里叶序列告诉我们,这些周期性信号可以分解为有限或无限的正弦波或余弦波的叠加,这些波的频率是原始信号频率的整数倍数。
在这里,这些波的基本频率代表直流系数,该系数称为振幅和相位。信号的波形可以根据幅度和相位逆变换来恢复,因此幅度和相位包含信号的所有信息。在这里,幅度是关于频率的,我们称其为频率频谱,相位是频率,我们称其为相光谱。
下图是将矩形波分解为多个正弦波的示意图。随着正弦波数量的增加,矩形波可以无限地近似。对于非周期性信号,我们不能简单地将其扩展为正弦波的叠加,但是我们可以将傅立叶变换用于正弦波的无数叠加,并且可以简单地获得表达式。
我们在日常生活中遇到的钢琴声音,振动等可以分解为正弦波的叠加,并且电路中的周期性电压信号和其他信号可以分解为正弦波的叠加。因此,问题是,为什么我们需要将信号分解为正弦波的叠加?其中有两个问题,我们为什么要分解它?为什么它是正弦波(或余弦波)?另一个问题是沟通学生。我们学会了多种转变。那么这些转变之间有什么关系?在下一章中,我将回答这三个问题。
为什么分解为正弦波叠加
在求解热传导方程时,可以追溯到傅立叶变换的创始人傅立叶,因为热传导方程要求读取器对热力学有一定的了解。在这里,我将以简单的谐波振荡器系统为例来说明此问题。可以通过以下微分方程来描述一个没有阻尼的简单谐波振荡器系统
它分别代表位移,时间,系统固有频率和外部驱动力。当没有外部驱动力时,该系统具有一般解决方案
现在,我们考虑存在外部驱动力的情况。那些熟悉普通微分方程理论的人可以知道,此时的一般解决方案是上述次级方程式(Cansure 0)加上特殊解决方案的一般解决方案。所谓的特殊解决方案是一定满足上述非同质秩序的满足。连接了任何一个方程(并非总是0)!那为什么要完成这种分解?原因是这是一个线性系统,或者该方程是线性方程,因此遵循叠加的原理,可以简单地证明这一总体结论。假设线性系统可以通过线性微分方程描述
它是一个线性运算符,您可以简单地理解为振荡器方程中的左手操作。如果它们是次级方程的一般解决方案和非均匀方程的特殊解决方案,则它们满足
然后添加这两个公式以获取
因此,对于给定的驱动力,只剩下一个问题,如何找到特殊的解决方案问题。也许您仍然记得,在高级数字书中kaiyun全站网页版登录,当它是三角函数和指数函数时,您可以拥有具有相同形式的特殊解决方案。例如,可以假定非均匀方程也具有这种形式的特殊解决方案,将它们替换为原始方程,并找到待定的常数以获得特殊的解决方案。指数形式的驱动力也相似。那么,我们如何找到针对其他形式的驱动力的特殊解决方案呢?这很简单。使用线性叠加的原理,如果我在正弦驱动力下找到许多特殊的解决方案,并且可以将其表示为这些正弦波的叠加,难道无法通过这些特殊溶液的叠加获得特殊的解决方案?在数学语言中,它是
如果上面的第二个方程的右侧相等,则左侧是原始均匀方程的特殊解。简而言之,它是使用傅立叶变换到驱动力(如果是周期性的驱动力,它将扩展为傅立叶系列),找到每个碱性驱动力的特殊解决方案,然后将其叠加以获得特殊解决方案。当然,您无需在实际解决方案中如此践踏。以简单的谐波振动方程为例,只需在方程式的左侧和右侧进行傅立叶变换并获得
上面表达的函数表示时域函数的傅立叶变换。这是一个代数方程式,很容易找到。
通过上述描述,我们可以看到,进行傅立叶变换或将函数扩展为傅立叶系列可以帮助我们解决线性微分方程,或者从实际意义上讲,可以帮助我们向外界分析线性系统如何响应!我们之所以能够以这种方式展开的原因是因为我们分析了线性系统。如果它是非线性系统,则不能这样运行。至于为什么它是三角函数,我将在下面回答。让我们看看更多示例。
傅立叶变换和信号系统
在这里,我们给出了与通信相关字段的另一个示例,以说明扩展到三角函数(或复杂的指数函数)的重要性。我们称这种分析傅立叶分析或频谱分析。
信号通常由时间的函数表示,这是如此简单和直观,因为它的功能图像可以视为信号波形,例如声波和水波等。多次,信号的处理非常特别。例如,在线性电路处理输入正弦信号之后,输出仍然是正弦信号,但是振幅和相位发生了变化。这是因为线性电路可以通过恒定系数的线性微分方程来描述。输入信号可以视为外部驱动力,并且可以将输出视为系统响应,该响应与上述振荡器方程相似。因此,如果我们将信号全部分解为正弦信号的线性组合(傅立叶变换),则可以使用传输函数来描述该线性系统。例如,如果此信号在数学上不存在,则引入拉普拉斯变换以解决此问题。这样的线性系统可以通过传输函数表示。因此,从中我们可以看到将信号分解为正弦函数(傅立叶变换)或复杂的指数函数(拉普拉斯变换)对于分析线性系统也至关重要。
傅立叶变换和量子力学
量子力学的波函数可以通过许多不同的表示形式来描述,例如坐标表示,动量表示,能量表示等。不同表示之间的转换实际上是希尔伯特空间的统一转换,其中坐标表示和动量之间的转换外观是傅立叶变换。
傅立叶变换,拉普拉斯,z变换,离散傅立叶变换之间的关系
通常需要进行各种转换以在信号处理中发出信号,其中傅立叶变换,拉普拉斯,z变换和离散的傅立叶变换是最基本的变换。他们都使用转换来对信号进行频谱分析,但是转换的信号会有一些差异。
如果您仅关心信号本身而不是系统,则可以通过以下过程链接这些转换之间的关系。
从模拟信号开始,如果模型信号的能量是有限的,那么我们可以进行傅立叶转换并在频域中表达它。如果信号的能量是无限的,则傅立叶变换将不会收敛。目前,可以在其上执行拉普拉斯变换。如果我们绘制拉普拉斯的场,它是一个复杂的平面,而拉普拉斯变换是该复杂平面上的复杂函数。该函数沿假想轴的值是傅立叶变换。
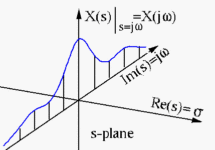
拉普拉斯变换和傅立叶变换广泛用于模拟电路分析。下图是模拟电路中基本组件的域建模的示意图。当时,这是傅立叶变换。
有必要澄清观点。无论是使用时域还是频域(或S域)表示信号,它们都代表相同的信号!也就是说,时间域的表达,频域表达和域表达最重要的是同一模拟信号。您可以从线性空间的角度理解这一点。如果将不同的坐标帧(或基础向量)用于同一信号,则它们的坐标将不同。例如,使用AS坐标,可以将信号表示为,并使用傅立叶变换的形式。在两个不同的坐标框架下,可以通过线性转换将同一向量的坐标链接。如果它是有限的尺寸空间,则可以表示为矩阵,它是无限尺寸,而这种线性变换是傅立叶变换。
到目前为止,关于信号形式的假设还没有太多。如果信号是带宽限制的信号,也就是说,它仅在较小的范围内(例如)而不是0。进行此假设的原因和此假设的合理性取决于实际需求。在通信系统或信号处理系统中,无法处理具有无限带宽的信号,并且通常在接收信号期间会有一定的带宽,因此这是实际信号的理想假设。现代信号处理系统主要是数字信号处理系统。现在,即使模拟系统也经常将复杂的处理放在数字信号处理子系统上进行处理,并且这两个系统通过AD和DA连接。根据采样定理,只要采样频率足够高(带宽的两倍以上),信号就可以恢复而不会失真。那么采样对信号的影响是什么?从S平面,时间域中的采样将沿虚拟轴方向定期扩展!该属性可以轻松地数学验证。下图显示了采样对信号频谱的影响,仅绘制虚拟轴上的图像。该属性还解释了为什么需要两倍的采样频率,以使频谱在延长后不会重叠。假设它是采样频率,采样后的信号可以在域中表示为
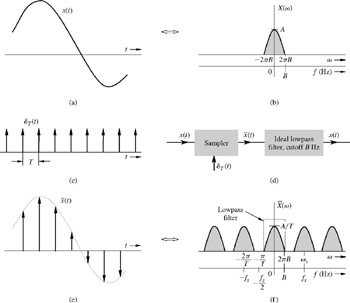
对于采样信号,可以使用指数转换将域的带状区域转换为单位圆。这是Z-Transform,可以被视为Laplace转换的一种特殊形式,即,它是采样频率。这种转换将信号从S域转换为Z域。请注意,S-域和Z域代表相同的信号,即完成采样后的信号,只有采样才能改变信号本身!从复杂的平面中,这种转换将平行于轴平行的条转换为Z平面的单叶分支,并将虚轴映射到单位圆。时间也称为离散时间傅立叶变换(DTFT)。您会看到,由以前的采样重叠引起的定期扩展产生的频段。由于周期性,z域中不同分支的函数值相同。换句话说,如果没有采样,并且直接执行Z变形,您将获得一个多价值的复杂函数!因此,采样后通常仅将z转换为信号!
在这里,我们谈论时域采样。在时间域采样后,信号仅具有两者之间的频谱,即最高频率仅是采样频率的一半。但是,要记录这样的信号,仍然需要一个无限的存储空间,并且可以进一步采样频域。如果时间有限的信号(实际上,这与频率限制相矛盾,但大多数信号大致是正确的),则可以从采样信号恢复原始信号,而不会通过频域采样(时域的周期扩展)来恢复。信号长度是有限的,它是离散的傅立叶变换(DFT),它具有著名的快速算法快速傅立叶变换(FFT)。为什么DFT如此重要?由于计算机需要有效地对一般信号进行傅立叶变换,因此除非信号具有简单的分析表达式,否则它们将使用DFT实现!使用上述关系,可以得出dft在KTH频率点的值为
上述推导使用两个基本公式
总而言之,对于线性系统,输入和输出是线性关系,无论是线性电路还是光学路径,只要可以通过线性方程或线性微分方程来描述它(例如拉普拉斯方程,poisson,poisson等式等。应用的两个著名示例是线性电路和傅立叶光学元件(信息光学)。在许多情况下,即使是非线性系统也使用线性系统!这就是为什么傅立叶变换如此重要的原因!您会发现,傅立叶是第一个解决热传导方程的人(实际上可以将其视为线性系统)。
傅立叶变换的想法在不同的领域中发生了多次演变,例如信号处理中的小波变换,这也使用了一组基础函数来表达信号,但它克服了傅立叶变换无法执行时间频率分析的问题同时。 。
解释傅立叶变换的特殊原因
最后开yun体育app官网网页登录入口,我将从纯粹的数学角度谈论哪些傅立叶变化是什么。如果我们将函数视为向量,那么这些函数在数字的加法和乘法的操作下形成线性空间。如果我们定义内部产品
还定义了该集合是有界函数的子集,所谓的有界界面指的是内部产物。然后上面提到的线性空间是希尔伯特空间。在这里,我们忽略了这些严格的功能分析中的定义,只是将它们与欧洲空间中的向量和内部产品进行了比较。在此类比中,一个函数是向量。
在此类比之下(严格的证明需要使用功能分析,在这里我们只关注直观的图像理解),傅立叶变换是该向量空间中的统一变换!我们知道,欧洲空间中的线性转换可以由矩阵A表示,即转换
这意味着向量X通过转换A转换为B!傅立叶变换将时域函数f(t)转换为频域函数f(w)!使用傅立叶变换的基本属性,很容易验证这种转换是一个统一的变换。
我们知道线性转换的本质是所选基础向量不同。向量的每个坐标是在相应的基础向量之前的系数!
那么功能空间的基础向量是什么?在时间域,基础向量可以被视为Delta函数
可以将这里的积分与以前的总和进行比较,可以将其与基础向量成为基础函数进行比较,并且可以将F(s)与基础函数之前的系数进行比较!
在相同的类比中,傅立叶转换为频域选择的基本函数是
f(w)是基础函数之前的系数。傅立叶变换是这两组基础函数之间的线性变换!
因此,问题是,线性转换如此之多,为什么傅立叶变换如此特殊?
记得线性代数中的线性方程式ax = b吗?解决该方程式有很多方法,高斯消除方法是最常用的方法之一。但是,如果A是对角线方形矩阵,则该向量版本的线性方程可以转换为多个独立的代数方程!
在这种情况下,很容易找到!
上述情况太特别了。我们考虑更普遍的情况。如果A是对称的方形矩阵,则根据线性空间的特征值理论,可以找到所有相互正交的特征向量和矩阵A的特征值,然后使用矢量X和B。 Represented as a combination of eigenvectors. Due to the orthogonal relationship of the eigenvector, the algebraic equation of the matrix can be transformed into n scalar algebraic equations
这不是很棒吗?呢A vector version of linear equations turns into multiple independent algebraic equations by reselecting a set of basis vectors!
Do you ask if this has something to do with the Fourier transformation? Don't worry, let's look at non-homogeneous linear ordinary differential equations
If the linear operator part on the left is regarded as a linear transformation, then this equation can be completely compared with the linear equation in the above vector version! Think of operators as linear transformation, can we adopt the above similar ideas and turn this equation into multiple independent algebraic equations?答案是肯定的。 Just use the feature function of this operator as the basis function to select the basis function again! It can be verified that the exponential function is the eigenfunction, and the corresponding eigenvalue is
Using similar ideas, our gate handle functions are represented as linear combinations of basis functions.
Then in this way, the aforementioned differential equation becomes multiple scalar linear algebraic equations!
In fact, this process can also be regarded as doing Fourier transforms on both sides of the original equation at the same time! This is also the theoretical basis for Fourier transform to solve the differential equation of constant coefficients!
Similar conclusions are also found in the linear partial differential equations of constant coefficients! For example, consider the active Laplace equation
Easy to verify basis functions (actually Green's function)
It is the feature function of the Laplace operator! Expanding the fields and sources according to the basis function can transform the original Laplace equation into multiple scalar algebraic linear equations
The above Fourier transform can also be replaced by the Laplace transform, the conclusion is the same! The above is what I experienced when I was taking the mathematical equation course. To sum up, Fourier transform is a special orthogonal transformation in linear space! The reason why he is special is that the exponential function is an eigenfunction of the differential operator of the constant coefficient! Most common laws in nature are described by constant coefficient differential equations, which are even more common in signal systems. Linear time-invariant systems can be described by constant coefficient differential equations, which makes Fourier transform very widely used!
Examples of feature functions of other differential operators
For the linear differential operator of constant coefficients, the exponential function can be used as the basis function, while for the linear differential operator of variable coefficients, its basis function is no longer a simple exponential function. However, the above ideas can still be used, but the basis functions are special functions, such as Bessel function, Lejeune's multi-nation function, etc.
The so-called constant coefficient differential operator is a differential operator with this form
For differential operators with variable coefficients, they are functions of independent variables, and there is no general conclusion on the characteristic functions of such operators. Basically, each type of operator will have its own special feature functions. Here are a few feature functions and variable coefficient operators that I have encountered many times.
Under the column coordinates are the characteristic functions of the following differential operators
Under the spherical coordinates
It is the characteristic function of the following differential operator, which is a differential operator with variable coefficients
有许多这样的例子。 These functions are actually a family of functions, and these functions are orthogonal to each other. This is the same as the properties of the eigenvectors of real symmetrical arrays. The linear operator here is also in its functional space. symmetric yoke operator. These function families form a complete set of orthogonal basis and can express any function in the corresponding functional space. This is the same as the basis function of Fourier transform - the complex exponential function.






