
为了进一步详细介绍傅立叶系列,本章介绍了新的知识点,
功能和卷积。为了介绍这两件事,我们有必要了解线性时间不变系统(LTI)。本章似乎有很多知识点。
信号和系统习俗写作:
连续信号:x(t)
离散时间信号:x(nt)
离散信号:x [n]
连续频域:
离散频域:x [n]
上面的n是整数,其他数字是实数。
所有时间域信号均在小写字母中,所有频域信号均在大写,[]中使用离散信号,并且在()中使用了非污点信号。
1。LTI(线性时间不变)
我们只讨论LTI,为什么? 1。困难,大多数人无法学习; 2。LTI足以应对大多数系统。应该注意的是,如果您在非LTI系统中,则不得轻松使用LTI功能。
1.1让我们先看线性
线性是线性代数中的线性性。数学家喜欢使用公式来描述线性变换。
连续信号:
对于系统,
响应是
,,,,
响应是
,用于输入信号
,如果系统响应是
,然后该系统称为线性系统。
离散信号:(将上述连续信号交换为离散信号)
对于系统,
响应是
,,,,
响应是
kaiyun全站网页版登录,用于输入信号
,如果系统响应是
,然后该系统称为线性系统。
线性概念在数学上乘以标量,并且输出也乘以标量。对于一个信号,输入信号的幅度变大的倍,输出信号变大的倍;
线性的另一个概念是叠加的概念。如果两个或多个信号被叠加,则系统的响应等于每个信号的原始响应的叠加。
1.2时间不变
时间不变的系统意味着系统的响应不取决于当前时间。例如,我早上9点在计算机上打开计算机,计算机打开了。这种反应与我对晚上10点启动的反应相同。由于启动时间不同,计算机不会有不同的响应,这被称为时间不变。例如,我在上午9点打开计算机,系统正常打开。当我晚上打开时,由于计算机是入口的,计算机无法打开,因此该系统成为了随时间变化的系统。由于系统不同,因此系统具有相同的输入。 ,响应是不同的。
数学家仍然喜欢使用美丽的简单公式来描述它:
信号
响应是
,如果
响应是
,然后系统是
时间不变的系统;
相应的
信号
响应是
,如果
响应是
,然后系统是
时间不变的系统;
在某些地方,离散域的时间常数称为移位常数。
当然,有些人会从哲学的角度否认“人们不能两次进入同一条河”的哲学角度。实际上,实时不变的系统仅存在于数学公式中。在现实世界中,从来没有一个严格的时间不变的系统,因为从长远来看,善意不可避免地会变得糟糕,而生活将不可避免地消失。因此,通常是在内部短期的假设,该系统是一个改变时间的系统。
该系统的其他功能暂时不会被描述,因为它们暂时没有使用,并且在需要使用时会被描述。
2。
2.1离散域
信号
让我们看一下离散域
信号。
离散域
信号是一个仅在n = 0和所有其他点等于0时等于1的信号。从数学角度来看,它非常漂亮。
根据定义,对于离散序列x [n],很容易获得
进一步,用任何整数替换上述1:
显然我们可以看到
该函数的一个独特特征是过滤特性,过滤所需的序列并过滤其余序列。此外,我们每次都从
过滤到
,然后将所有过滤掉添加以获得原始序列。数学表达是:
因为
,因此上述公式进一步写成
来回走kaiyun.ccm,上述公式是信号
可以用信号本身制成
获得信号卷积。证明过程在上面,我们将看看以后的卷积。
2.2连续域
功能
将这个离散域定义明确的信号扩展到连续函数时,似乎很难实现。如何定义一个仅在0点的函数,而非0分为0?在数学中,似乎可以将断点定义为此。这种定义显然对连续功能没有物理意义。根据此定义,该函数的能量为0。在连续域中,由于只有一个中断点要使用,因此能量为0。嗯,经过仔细考虑,数学家给出了以下定义:
显然,它具有能量,但这也是一个相当异常的定义。从积分的意义上讲,函数的面积为1,但其宽度为0,因此该函数的高度应无限。想象一下,在时间轴上,一个功能,
t =
当它是0;当t = 0时,它突然变得无限。然后
当该函数的值再次变为0时。
功能就是这样的函数。
对于这样的功能,需要使用最终方法来实现物理。定义矩形或三角形,然后使其基本边缘长度趋于0。显然,没有这种信号。
在离散域中,
信号具有过滤特性;在连续域中,我们更改名词,称为采样特征。相似的
,由于连续域
该函数还具有积分1的属性,因此具有以下属性
经过
我们可以采样功能
随时值。
有
对于信号,我们可以链接x [n],x(t)和x(nt)(量化),并且可以在采样和量化后量化离散信号(此处暂时忽略了量化)。
通过采样和量化,连续模拟信号成为一个离散的数字信号,可以通过数字信号的处理方法进行处理。处理后,将数字信号重建为模拟信号。整个过程是数字信号处理过程。
3。卷积
最后,这是关于卷积的。卷积似乎是一个学习困难。
卷积的引入应首先从离散域中考虑。
3.1离散卷积
返回第2.1节中描述的公式:
,这个公式显然是正确的。当您在右侧汇总并扩展Sigma时,它自然等于左侧。我当时说,该方程的另一个重要意义是它代表卷积公式,该公式代表序列x [n]和
信号卷积后,它也等于自身。
注意这个公式。第一项的系数和第二项的系数为n,即序列x [n]的n,然后等式的右侧是卷积,k消失了,最后只有n是左边。
在此基础上,将序列x [n]输入到系统H中,并且获得的输出为y [n];假设
代替
得到,
因为它是一个线性系统,所以
表示振幅,因此
记住
,那是
(这是由于时间不变的特征),因此有著名的卷积公式:
也可以写
其中h [n]是系统对
信号响应(也称为H [n])是系统的影响响应。
让我们从字面上解释这个公式。
在解释卷积公式之前,首先澄清概念。如果该概念没有澄清,它将始终感到困惑。
h [n]是指序列中的序列或特定项吗?对于n的不同理解,对卷积的理解是完全不同的。当将H [n]视为特定项目时,互联网上会有各种非常令人兴奋的解释,例如抛出颜色/肿胀的脸部等,核心是反向,翻译,乘法和累积的。我会短暂地重复一遍。
3.1.1 y [n],h [n]被识别为特定项目
在此前提下,让我们举一个简单的例子,想象下图中的输入信号x [n],系统的影响响应为H [n]。
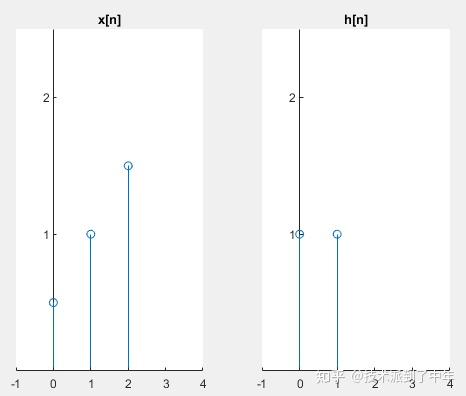
在此系统中,输入信号分别具有3个有效值x [0],x [1]和x [2],分别表示时间0,时间1和时间2的输入;影响响应具有两个H [0]和H [1],H [0]表示系统0延迟的响应,而H [1]表示系统延迟1的响应。
步骤0,计算y [0],我们只需要注意x [0]信号的h [0]的响应x [0],输入为0次,延迟为0,因此系统是在0时响应y [0] = x [0] h [0]; (请注意,信号的输入时间和延迟时间为0)
步骤1,计算y [1],我们需要注意时间0的系统的输入X [0]信号,该信号的响应x [0] h [1],延迟为1;输入X [系统1]信号的X [1]信号,其响应x [1] h [0]延迟为0;其他信号的响应无法满足时间1的输出,因此y [1] = x [0] h [1]+x [1] h [0](在这里请注意信号的输入时间之和延迟时间为1)
步骤2,计算y [2],0时间的输入。由于没有响应,延迟为2,因此不需要考虑0输入;对于1处的输入,其0延迟响应显然不会到达2个系统,其1延迟响应对y [2] x [1] h [1];对于时间2的输入,其0延迟响应将具有输出,并在时间2上贡献贡献值。它是x [2] h [0];此外,没有其他信号响应可以满足时间2的输出,因此y [2] = x [1] h [1]+x [2] h [0](请注意,请注意信号的输入时间之和延迟时间为2)
步骤3,依此类推,我们可以得到y [3] = x [2] h [1]+x [3] h [0]。
进一步,在n瞬间,对那一刻的响应是...
,...,,
,...,加起来
3.1.2 y [n],h [n]被识别为序列。在这里,n是一个变量开yun体育app官网网页登录入口,因此x [n]是一个序列。其他符号(例如x [k])被认为是一个特定术语。 。使用第一个项目,让我们再次看一下x [nk],那就是通过k单位延迟序列x [n];相反,x [n+k]是x [n]序列。
让我们看一下公式
,从时间0开始,x [0]代表时间0的强度x [0]的冲击信号,因为
冲击响应为H [n],因此X [0]强度的冲击信号产生的响应为X [0] H [n];同样,x [k]表示k时间的强度为x [k],例如,影响信号的响应是延迟k的单位,即x [k] h [nk];通过数学归纳,我们可以添加所有信号的响应
,,,,
,,,,
,...
,....,现在
。
给栗子
对于系统,影响响应是
也就是说,一种影响,这在通过系统后变成了两种影响。
仍然使用上面的x [n],然后
,我们逐步增加,然后添加以获取下面的图片。
从上图,我们可以看到x [0] h [n-0]计算y [0]和y [1]的一部分,x [1] h [n-1]计算x [1]的一部分。是Y [1]和Y [2]的一部分。可以看出,在不同的先决条件下,我们对同一公式有不同的理解。经过真正理解,您实际上会发现两个理解的本质是相同的。
改变观点
对于在输入处的影响响应为x [n]的系统,其输出y [n]是什么?
这等同于再次审查插图的过程,每个人都很高兴看到它
这是卷积的通勤定律。
实际上,数学家不需要画这么多的图片。数学家最擅长的是公式转换,让我们看看:
,令m = nk,然后k = nm,替代
,所以
。
简单是美丽,数学家不需要任何额外的东西。
另外,对于长度为m和n的序列,卷积后,长度为m+n-1。例如,在上面的示例中,m = 2和n = 3,卷积后序列的有效长度为4。证明很简单。对于长度为m的序列,它需要延迟(0次,1次,...,n-1次),最终长度为m+n-1。
让我们看一下连续的域
3.2连续卷积3.2.1定义
在本节中,我们从定义开始。
对于系统h,
响应是
,记得为
相应地
,系统响应是
在第2.2节中,我们得到
,在这里继续使用一些数学提示并尝试替换:
,,,,
,我们得到
,因为
,所以
, 代替
只是得到
因为我们的系统是线性的
表示振幅,因此
而且因为我们的系统是恒定的,并且
,全部
,所以继续有
上述公式是连续域的卷积公式。
3.2.2离散连续,使用最终方法
,首先审查离散公式。当更改为连续域时,我们将输入x [n]序列中的特定项x [k]更改为高
宽度是
小脉搏。用于离散影响响应
,其输入是1
信号;对应于连续域,我们将连续面积为1
信号,其影响响应是
,因此比较离散公式并一一替换它,我们可以得到
,制作
,你可以得到
此外,如果系统是因果系统(没有输入,没有输出,那么系统是因果系统),则因果系统的T时间输出不取决于T时间后的输入。
在因果系统下,
可以这样记住这个公式:系统中某个时刻的输入
,对于此输入,它相对于时间0延迟了
时间单元,因此其响应也应延迟同一时间,即
,始终累积并总和输入并获取输入。
此内存方法实际上与我在3.1.2中描述的方法相同。
下次我会再次调情。






