上一个博客介绍了音频字段的简单基础知识kaiyun.ccm,并提到了傅立叶变换。然后,该博客重点介绍了如何在抽样后使用傅立叶变换进行离散序列,这也是各种语音算法和前端处理的基础。
第一个重要的一点是周期性采样字符串及其傅立叶变换。我们要提及周期性采样字符串的原因是因为它是连续信号和离散信号之间的桥梁,并且因为它的傅立叶变换也是频域中的周期性采样字符串,可用于离散和定期信号。
周期性采样字符串是添加以t作为周期的无限δ函数。 δ函数是一个单数函数,可以在很短的时间内将其视为具有无限值的函数,但积分为1云开·全站体育app登录,周期性采样字符串可以定义为
通常,在离散的信号处理中,我们将撞击函数以1作为δ函数使用,而无限的δ函数周期形成了周期性采样字符串。周期性采样字符串的最大属性是其傅立叶变换也是定期采样字符串,因此可以实现时频域采样:
为了在t周期期间采样连续的时域函数,直观的方法是用周期性采样字符串将此连续函数乘以:
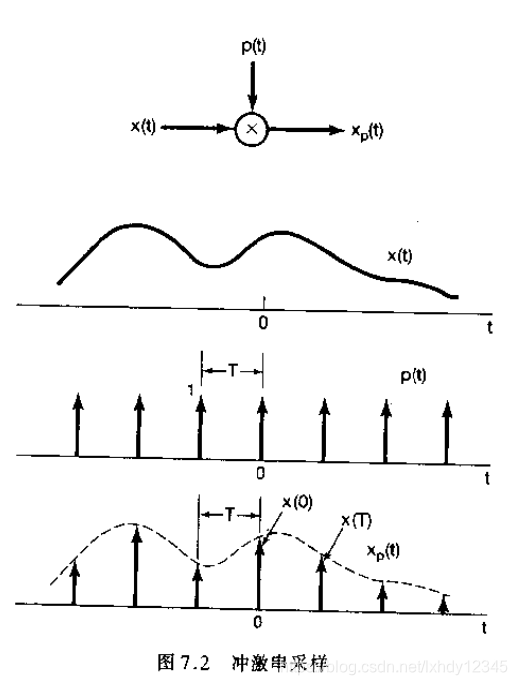
因此,我们可以使用连续的时间信号
获取离散信号:
在此离散信号上进行傅立叶变换可以获得离散时间的傅立叶变换:
![X_{p}(w)=\int (\sum_{t}x(nT)\delta(t-nT))e^{-jwt}\mathrm{d}t \\ =\sum_{n}x(nT)\int \delta(t-nT)e^{-jwt}\mathrm{d}t \\ =\sum_{n}x(nT)e^{-jnwT}\\= \sum_{n}{x(n)e^{-jwn}}\\= DTFT[x(n)]](/uploads/allimg/20250223/1740247339984_5.gif)
这是离散时间傅立叶变换(DTFT)的形式。通常,这里将在这里省略。当然,应该注意的是,每个离散时间序列的值(数组)包含一个采样周期。时间是离散的,但是上述方程需要计算无限时间n的总和,并且仍然无法在一个上计算计算机,因此我们需要分离信号的频率。在这里,我们需要使用δ函数的采样属性,即使用连续的时间函数的δ函数的卷积可以获得此函数的相同输出,只是有时间移位。
连续函数卷积可以定义为:
因此,在NT处的δ函数的卷积以及连续的时间函数可以提取NT函数的值:
因此,可以通过周期性采样字符串和时间函数进行时间函数进行周期函数:
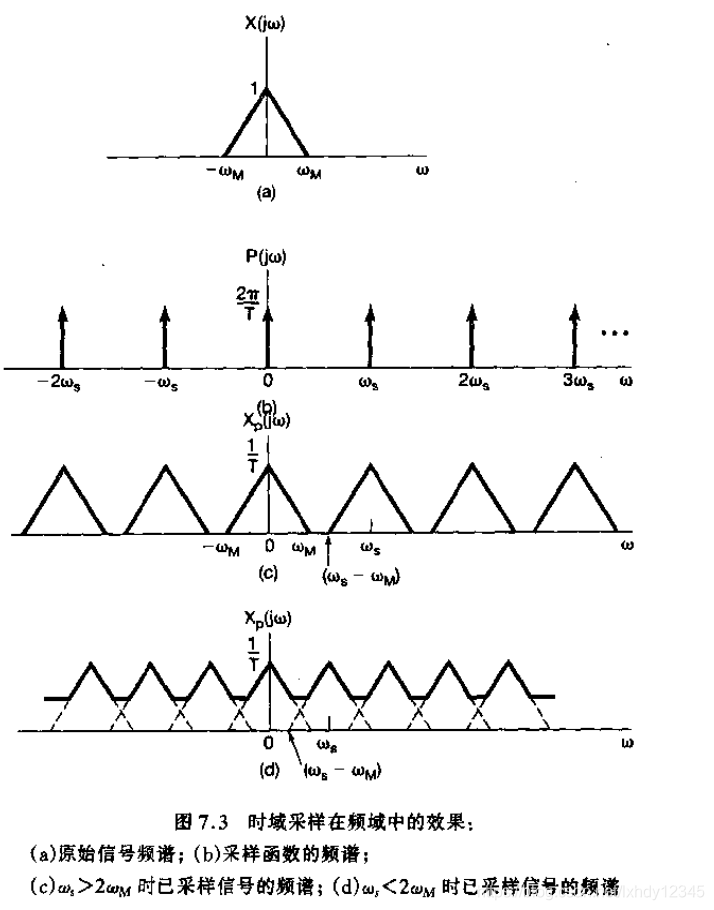
通过时间域的分期,频域可以离散。这是因为时间域的卷积在频域中乘以。因此,时间域的周期是要转换原始函数的频谱和频域中频域中的周期性。乘以采样字符串可以在频域中获得离散性,因此可以解决离散的傅立叶变换。在这里,我们假设上面的时域周期性采样字符串的采样周期为T0,我们希望执行T1的定期扩展时间域信号。假设T1 = NT0,用于周期扩展的周期性采样字符串可以定义为:
它的离散时间傅立叶变换是:
省略采样周期T0,然后切换总和符号:
因为有这样的公式:
因此,什么时候
当它是0时,也就是说,当只有实际项1时,其傅立叶变换是:
将上述方程式乘以离散的时间傅立叶变换公式以获得离散的傅立叶变换:
![DFT[x(n)]=DTFT[x(n)*\sum_{m}{\delta(n-mN)}]\\= DTFT[x(n)]\sum_{k}{\frac{2\pi}{N} \delta{(w-\frac{2\pi}{N} k)}}\\ \\=\frac{2\pi}{N}\sum_k X_{p}(w)\delta{(w-\frac{2\pi}{N} k)}\\=\frac{2\pi}{N}\sum_k\sum_{n} x(n)e^{-j\frac{2\pi}{N}nk}](/uploads/allimg/20250223/1740247339984_16.gif)
要需要相应的频点K,它是:
这是离散傅立叶变换(DFT)的公式。可以发现该公式在频域W中是离散的。我们将一个周期的频域分为n个部分,我们只能求解其中的kth。 /n频率成分响应。
上述DFT形式可以写为以下矩阵乘法形式。 n点的傅立叶变换可以将n点的时域信号更改为n点的频域信号:
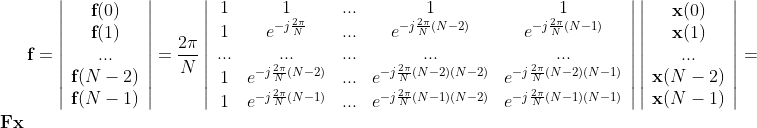
这也是计算机求解傅立叶变换的主要方法,但是由于有两倍的总结,因此上述矩阵乘法的复杂性为O(n*n),因此解决超长的傅立叶变换很昂贵。快速傅立叶变换方法(FFT)降低了求解上述矩阵乘法到O(NLOG2(n))的复杂性,这也是傅立叶变换方法真正输入大型应用程序的基础。优化上述傅立叶变换乘积的方法主要是通过转换矩阵的对称压缩来计算量,如果有机会,我们将在稍后讨论。这种转换矩阵F非常漂亮。它是一个复杂的矩阵和一个统一矩阵。也就是说,乘以F的共轭换位,其本身可以获得一个单位矩阵,并且其共轭转座等于其反矩阵。通过简单的计算,您可以找到以下方程式:
因此,获得逆离散傅立叶变换
这很简单,只需在上述转换矩阵上执行共轭转置操作即可。
在此过程中,我们需要注意几个问题:
1。在上述离散过程中的采样率问题,频域中的采样间隔为
,等同于将一个段分为n个细分市场,决议是
,我们无法计算低于此频率的组件的大小。在上面的第二个图中,它是时间域的混叠,因为功能周期大于周期周期。 (在频域中,图片在频域中混为一谈,这里谈论在时间域中的混叠)
2实际上,还有另一种扩展方式,这不是周期性扩展,而是对称扩展。所得的转换是离散的余弦变换DCT,这也是非常重要的转换。优点是转换位于实际数字域中。
3执行上述周期性操作后,原始序列移位将成为循环移位,序列翻转将变成对称翻转(位置0处的序列保持不变,其他对称翻转将逆转)。
4最重要的特征是共轭对称属性,它仅谈论转换矩阵上的性能。具体而言,对称性如下:
对称性的优点是,可以使用n点FFT计算2N点真实信号的FFT。简而言之,我们只需要使用2n点信号作为奇数及其偶数的新复杂信号的真实和虚构部分组件和该共轭的输出是原始两个真实信号的FFT。
这似乎只是一本书中的数学转换,但这对实际应用至关重要,因为一般而言,这两个频道的左右通道的信号按左一个顺序排列在缓存中,并且一项。使用上述方法可以同时处理两通道的傅立叶变换,这也被认为是实际处理中的一个小技巧。
5最后,让我们谈谈转换矩阵。此转换矩阵是线性变换。使用N输入,有N输出。要使用卷积神经网络的结构,有n n卷积内核,但是由于它很复杂,因此存在2N真实的卷积内核,其中n是正弦基础n是余弦的基础开yun体育app官网网页登录入口,也可以在中实现傅立叶变换。通过具有2N卷积内核的一维卷积层,例如张量和其他框架等框架。一般而言,2N实数基础的卷积计算是完整的,并且超过2N的卷积内核过度完整。这种转换不仅是传统上基于端到端语音模型(例如Conv-Tasnet等)。傅立叶变换模型具有更高的性能。






