目录
目录
1频率域傅立叶级别的周期性信号的概述1.1傅立叶系列周期性线性信号
傅立叶分析了:
时间连续的,任意的周期性时间域信号可以分解为无限多个,离散,非周期性,正交复合物指数频域信号的总和,称为傅立叶级数。
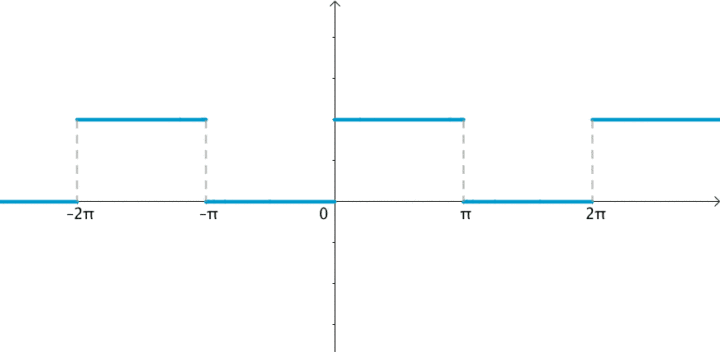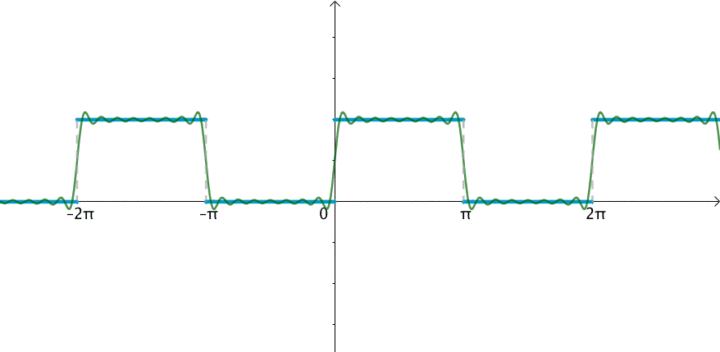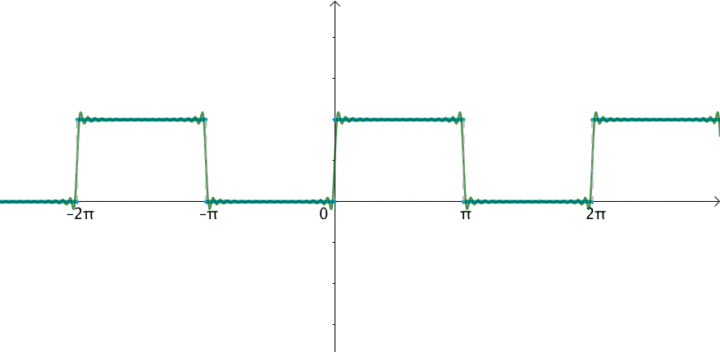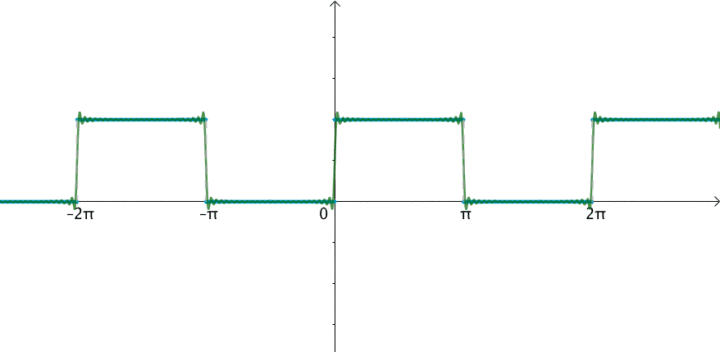
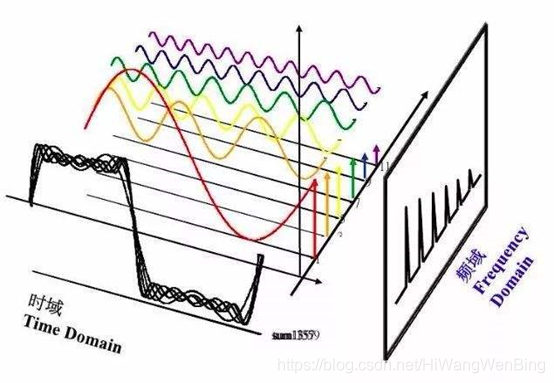
为什么得出这个结论?
从定性的角度来看,周期性信号是常规的复杂信号,而正弦信号序列cos(n*ωt)+i*sin(n*ωt)具有多个频率关系的基本信号。
使用不同振幅的无数正规和基本信号来获得常规且复杂的周期性信号是可行的。
傅立叶系列1.2个时期,离散信号

傅立叶分析了:
时间滴定,任意的周期性时间域信号可以分解为无限多重,离散,周期性,正交复杂的指数频域信号的总和,称为离散傅里叶序列。
也就是说,周期性离散信号的频谱比连续信号的频率频谱更正常,并且已成为周期性信号。
频谱的所谓周期性是指不同频率成分振幅的周期性,并且与周期性连续信号不同,频谱没有周期性。
1.3非周期连续信号
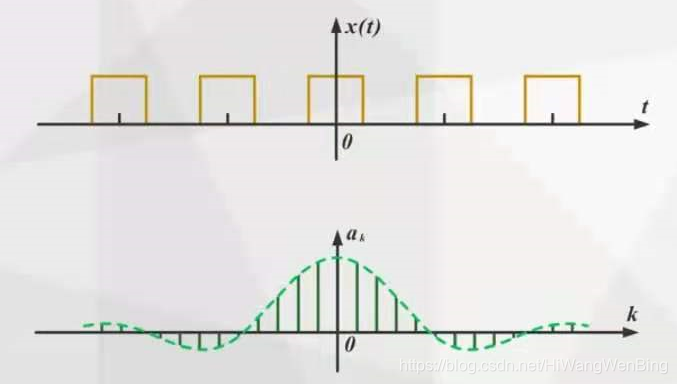
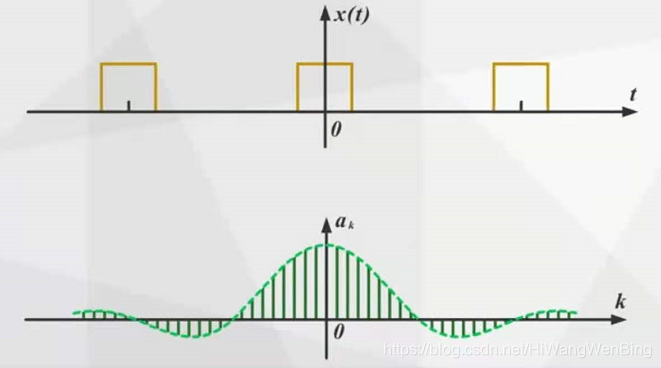
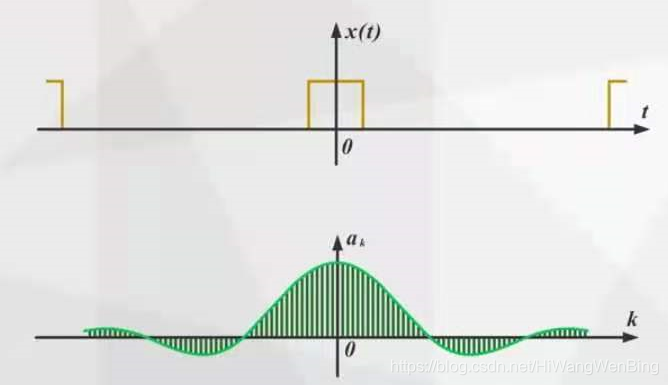
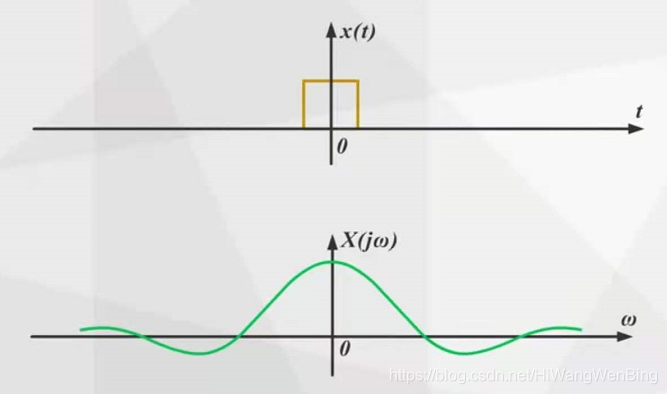
傅立叶认为,时间域中非周期性连续信号的光谱可以从该时期的连续信号的频谱中得出。
当域信号的周期是无限的时,周期性信号变成了一个非周期性信号。无限周期,这意味着时域信号的频率很小,这意味着基本频率无限小,与此同时,这意味着两个相邻的谐波信号之间的间距是无限的,并且间距为无限小,这意味着谐波频率变得连续。
还可以理解,定期信号是常规信号,因此可以通过无限,离散,谐波信号组合它们。当它们成为不规则的非周期信号时,需要组合更多的谐波信号。 ,在整个数字轴空间中,谐波频率是连续的!
2。傅立叶系列时域,周期性,连续信号频域的频谱图2.1周期性频谱图,连续信号
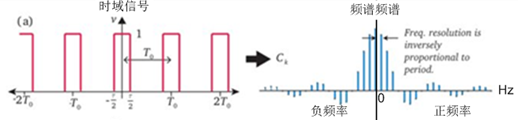
周期性连续信号有2个重要参数:
t>τ
(1)时域信号
右侧是时域信号,这是周期性脉冲信号。
(2)频域频谱
右侧是相应的傅立叶级数的频谱图kaiyun.ccm,代表了时域信号中包含的不同频率的复杂索引信号(SINE信号)的频率n*ωt及其相应的振幅。
有关复杂索引信号的负幅度和负频率,请参阅:
“ Star Fire-35:为什么傅立叶分析需要引入负频率?负频率的物理意义是什么?》 csdn
2.2周期,离散信号的光谱图

定期离散信号有两个重要参数:
n> n1。
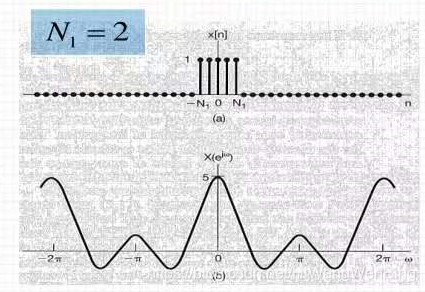
以下是当n = 20和n1 = 2:当离散方波信号的频谱图:
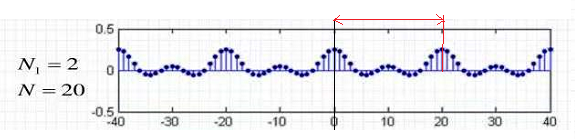
从上图可以看出:
这就像一个周期性的连续信号,表明时域信号中包含的谐波频率是离散的。
这与周期性的连续信号不同。每个频率分量的幅度正在减少kaiyun全站网页版登录,没有周期性。
至于定期离散信号,每个频率组件的幅度定期变化。
周期的大小取决于两个相邻采样点之间的时间间隔。
采样时间越小,离散点越密集。
采样频率越大,当采样点无限密度时,它接近周期性的连续信号,并且频谱周期接近无穷大,也就是说,它呈现出周期性的非周期性特征连续信号。
这与周期性的连续信号不同。周期性的连续信号,即在一段时间内,连续信号的采样点等效于无限。因此,尽管它们的频谱是离散的,但谐波组件的数量是无限的。
周期性离散信号中的采样点的数量是有限的,因此其频谱也是有限的。有限性反映在其周期性中。光谱的谐波成分的数量是光谱期间的谐波。波数。
频谱的有限性是定期离散信号的重要优势。通过有限的谐波频率,可以复制周期性离散信号,从而节省网络带宽。
时间域中的离散率是定期离散信号的另一个非常重要的优点,而连续信号集成的积累和更换对于计算机处理非常方便。
定期离散信号是计算机数字通信中最重要的时域信号。
在计算机数字信号处理中,对于连续信号,首先通过采样将连续信号转换为离散信号。抽样后,它不仅有助于计算机处理,而且还节省了恢复信号所需的光谱资源。
2.3非周期,连续信号

从频谱中,时间域中基本信号的频率无限接近0,并且相邻谐波信号的频率间隔接近0,这是连续的。
2.4非周期性,离散信号
时间域的多个焦点导致频域频谱的连续性,要求无线连续的谐波组件在时间域中结合不规则的上的上静脉信号。
时间域中的离散率会导致频域频谱的周期性和规律性,这是时间域中离散率的好处。
3时域,周期性,连续信号三角函数表达连续信号的傅立叶系列频域3.1周期性,连续信号
假设时间域周期连续信号F(t)的周期为t
该系列公式表明,时域信号F(t)可以由频域中的无数正弦信号组成。
3.2定期,离散信号
3.3非周期性,连续信号
3.4非周期性云开·全站体育app登录,离散信号4时域,周期性和连续信号复杂指数表达式4.1周期性,连续信号
该系列公式表明,时域信号F(t)可以由无数频域中的复杂指数信号组成。
4.2定期,离散信号
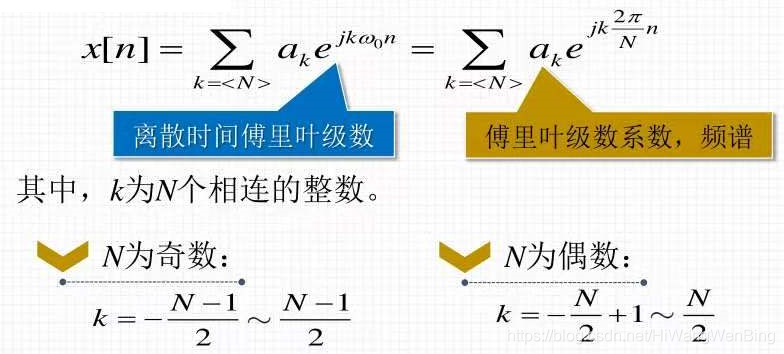
(1)傅立叶级数复杂索引信号集
(2)傅立叶级数复杂索引表达式
4.3非周期,连续信号

上述数学表达式表示:
时间域中没有常规的非周期连续信号,带有无限的谐波信号
构成,每个信号的频率ω是一个连续的,无限小或没有间隔,因此n =》dΩ,因此每个谐波信号的幅度不再离散,并且是连续的,由x表示(jw(jw) ),因为没有谐波频率,所以没有时间间隔,因此集成是
更换累积和
。
4.4非周期性,离散信号
非周期性和离散信号可以从周期性和离散信号演变,从而将定期离散信号的时期延长到无穷大。

5定量傅立叶串联参数5.1周期性连续信号
为了简化讨论,我们以正频率为例。负频率与正频率对称。如果存在正频率ω,则存在相应的负频率-Ω。
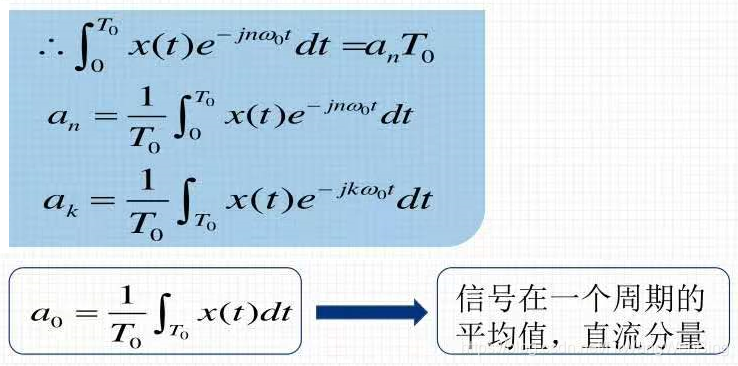
(1)频率定量:
(2)振幅定量

5.2定期,离散信号

5.3非周期性,连续信号
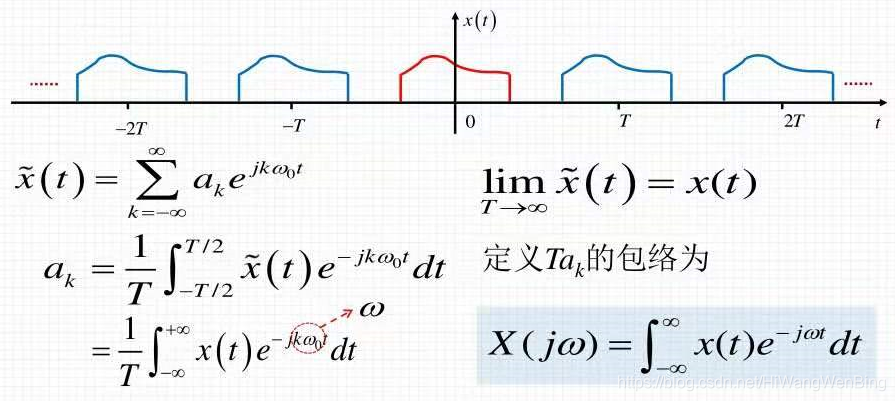
由于非周期性连续信号的光谱是连续的,因此其幅度不再由AK表示,而是由X(JΩ)表示,X(JΩ)是JΩ的复杂变量函数。
5.4非周期性,离散信号
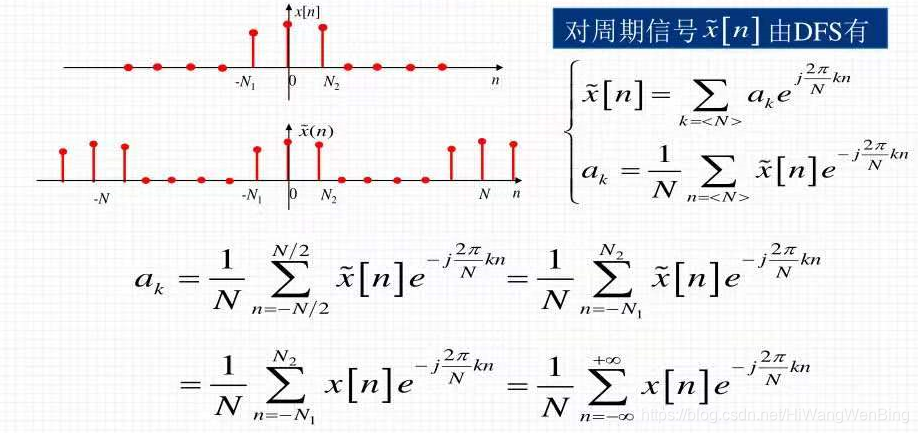
6个频域傅立叶级数均为普通时间域,周期性和连续信号6.1周期性连续信号
(1)普通正弦函数的光谱图

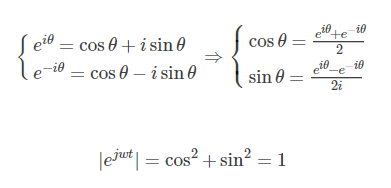
单个频率正弦或余弦信号,也称为单音信号。
它可以由三角函数表示,并且此时的光谱是单个正频率。
正弦信号或余弦信号本身也可以用一个复杂的索引来表示:包括一对具有相同绝对值和相反符号的频率。
(2)周期性矩形脉冲信号
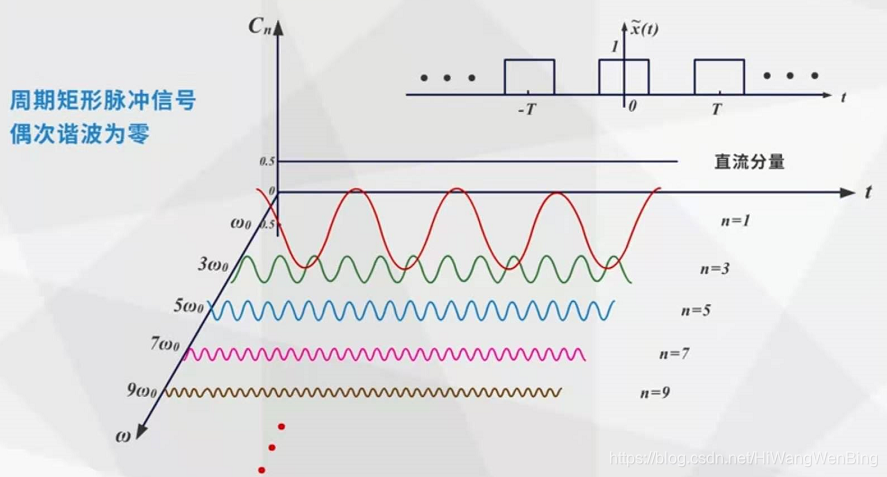
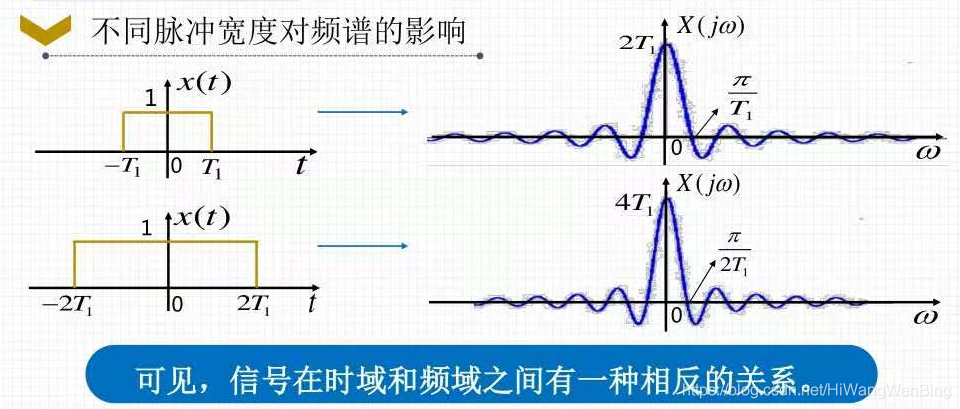
脉冲宽度保持不变,时域信号的周期t变化,频域信号的基本频率以及每个谐波信号的频率。 t越大,基本频率越小,谐波频率越密。
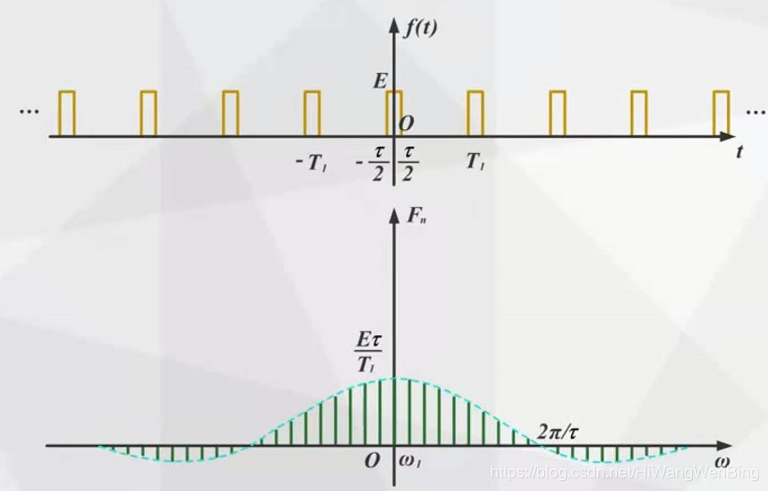
该周期保持不变,时间域信号的脉冲宽度t会影响周期t内的时间域信号的积分值。t越大,能量越大,一个星期内就越大,每个谐波分量的振幅就越大。
(3)周期性三角脉冲信号
6.3非外围连续信号
(1)冲击脉冲信号

在时域,持续时间是无限的。
查看频域,包含所有频率值的谐波是连续的。每个谐波频率的幅度为1。
它也可以理解为:脉冲信号是一个脉冲信号,即立即发生并立即消失,因此其频率无限变化,因此包含所有谐波组件,其频率值从0到无穷大。
(2)DC组件
从时域开始:可以将其视为具有无限周期的信号信号,导致其幅度值不变。
查看频域:因为信号的幅度保持不变,这意味着该域中的信号不包含任何会在频率ω上改变的交替的AC组件,这意味着它仅包含具有频率ω= 0的组件,即DC组件。
这就是为什么在频谱上只能看到ω= 0时的幅度。
(3)单位矩形脉冲

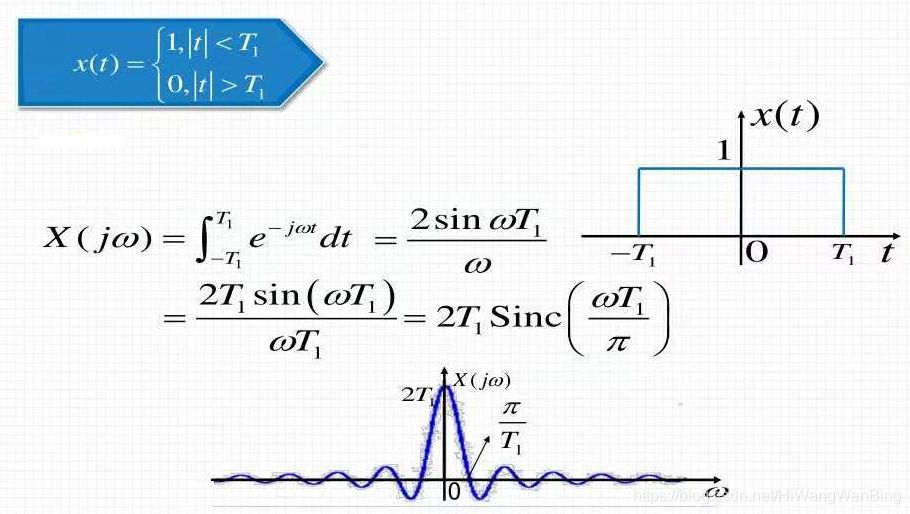
显然,单个矩形脉冲与周期性矩形脉冲:
相似性:图的信封相似。它们都是SINC函数,即歌手的功能。注意:不是犯罪功能。
区别在于,单个矩形脉冲的光谱是连续的,并且周期性矩形脉冲的光谱是离散的。
6.4大变化信号
(1)单位脉冲信号
(2)矩形脉冲信号
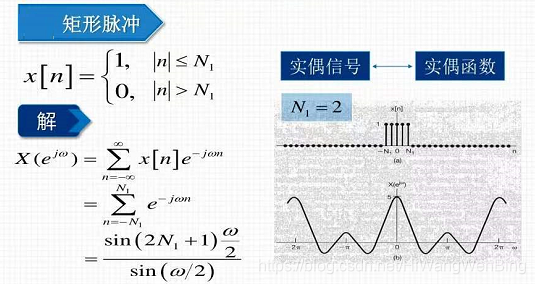
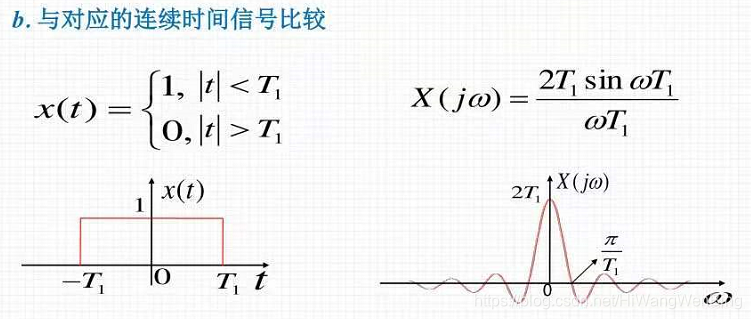
其他参考文献:
(1)SINC函数
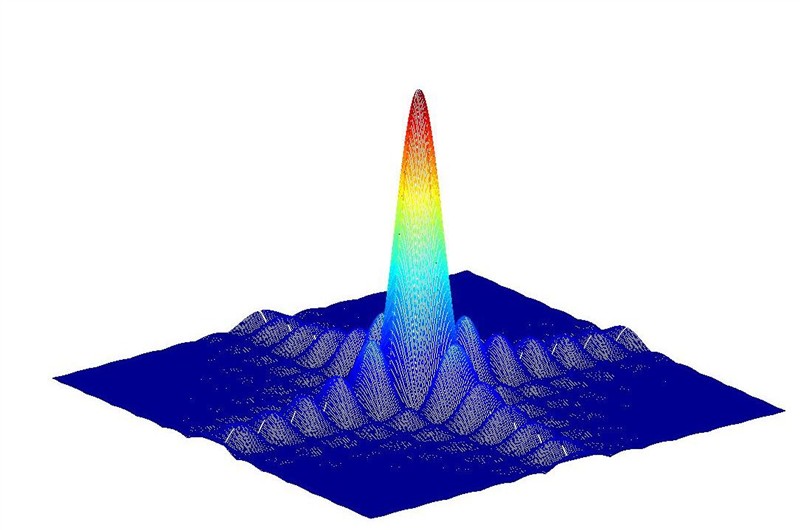
(2)不同转换的摘要







