在过去的千年中,从汉朝到唐朝,出现了许多算术书,最著名的十本书被共同称为“十本算术书”:“ Zhoufeng Arithmetics”,“算术算术的九章”和“ Saidao” “计算经典,Zhang Qiujian计算经典,Xiahou Yang计算经典,五个经典计算经典,古老的计算经典,“享受古代计算经典”,“享受技术”,“五个CAO计算经典”和“ Sunzi Cartulation Classics Classics” “,其中最著名的是“算术的九章”。

“算术的九章”是古代中国的第一本数学专着,也是“十本算术书”中最重要的一部分,该专着建于公元一世纪左右。作者不再验证。人们普遍认为,过去已经由多个学校添加和修订云开·全站体育app登录,并逐渐成为当前的固定版本。西汉王朝的张·坎格(Zhang Cang)和根奇(Geng Shouchang)曾经添加并整理出来,但当时它基本上已成为固定版本。最后一本书是在最新的东部汉朝早期写的。今天流传的大多数人是在三个王国时期的魏族皇帝皇帝(263)的第四年开yun体育app官网网页登录入口,而刘·福(Liu Hui)写下了“九章”的注释。
“算术九章”的内容非常丰富,该书总结了交战状态时期,秦朝和汉朝的数学成就。同时,“算术九章”在数学方面取得了独特的成就。它不仅提到了最早的分数问题,而且还记录了诸如利润不足之类的问题。 “方程式”一章在世界数学历史上也是第一次详细阐述了负数,加法和减法。算法规则。这是一项全面的历史工作,是当时世界上世界上最简洁,最有效的数学。它的外观标志着中国古代数学的完整体系的形成。

这项工作包含246个数学应用问题,属于九个章节:方形,玉米,CUI,SAP,商业成就,相同的损失,利润不足,方程式和句子库存。
例如,在“算术的九章”中,毕达哥拉斯分会带领贾(jiā)到达岸上:
原始文字:“现在有一个池塘是一个张的尺寸,芦苇在中央生长。一英尺的水出来了,它将芦苇带到岸边,这与海岸一致。询问。关于水的深度和芦苇的长度。”
翻译:有一个脚正方形的水池。游泳池中有一个新生的芦苇,该芦苇在水面以上是一英尺。如果将其定向到岸上,则与海岸完全齐平。水有多深,芦苇多长时间?
这个问题在世界数学史上具有很大的影响。古代印度数学家Poshgaro的《 Rirovati》一书包含“风向红莲花”,这是从这个问题中改编而成的;阿拉伯数学家凯西(Al Kathy)也有类似的“池”中等草的问题。欧洲书籍“ 16世纪算术”中的“圆池芦苇”的问题。他们比我们国家晚了数百或数千年。
注意:(1)Jia:发音为Jia,一种音调,发音与“ Jia”相同。新生的芦苇。 (2)一个张等于十个张。
该图如下所示。贾安·D(Jajian D)被带到岸上B点。在此过程中,据信芦苇不会在根A周围弯曲和整体旋转。A是从水C到岸的垂直距离,a = 5(脚); AC = B是水的深度; ba = da = c是芦苇的长度。 dc = cb,这是芦苇裸露的水面部分的长度,cb = 1(线)。显然,三角形ABC是一个右角三角形,C是斜边。
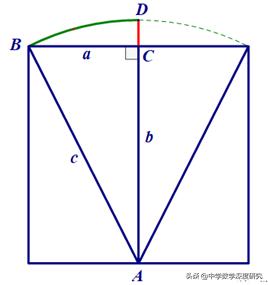
“九章”中的解决方案是:“多个半池塘,乘以一英尺的水,然后减少。让芦苇久远。”将其转换为公式
将相应的已知数量直接替换为上述公式
也就是说,水深为12英尺。芦苇的长度很容易找到,它的长度为12英尺,1英尺等于13英尺。在中国古代,人们希望找到最直接的计算公式,该公式是通过已知数量给出的,因此他们可以将其直接替换为已知数量以找到未知数的数量。
那么您如何获得此公式?我们知道,在右三角形中,如果已知直角边缘并且斜边和另一个直角边缘之间的差异,则确定此直角三角形。可以肯定的是,我们自然可以找到倾斜和未知的右角边缘的长度。这就是这个公式的含义。
让我们从毕达哥拉斯定理得出上述公式。
从上图中,显然有:
我们需要找到一种使已知数量CB出现的方法。如果您在上述公式的左侧使用平方差公式,则可以获取CB,但也可以获取C+B。 C+B不是已知数量,我们不希望它出现在最终公式中。我们试图找到一种方法来获取(CB)的正方形。如下所示:
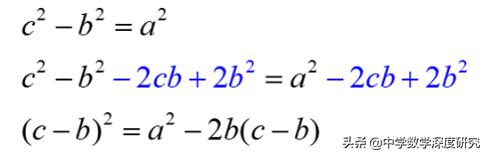
使用此配方,如果芦苇接触到水面2英尺,您会发现水深B为(25-4)/4 = 5.25英尺kaiyun全站网页版登录,芦苇长为7.25英尺。

使用此公式,可以解决其他类似的问题。 “算术九章”也给出了类似的问题
''圆形材料被埋在墙上了”,“现在壁上埋在墙上,他们不知道大小。用锯,一英寸深,一英尺长。询问道路? “
该图如下所示。圆形材料是指圆柱木或石头。以下是横截面的视图,这是一个圆。下弧BDE代表外部暴露的气缸,上弧BFE代表埋在墙中的圆柱体,我们看不到。原始标题中提到的“一英寸深”是指DC的长度; “一英尺长”(1英尺等于10英寸)是指BE的长度,其中一半是BC,即右三角形的右角边缘A = 5(英寸)。图中的B是从横截面到壁的中心的距离交流。图中的C是横截面圆的半径。
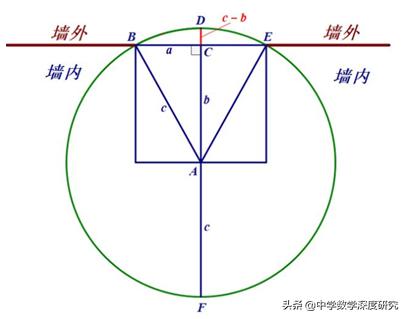
通过上述解释,我们可以应用上一个问题的公式以找到b的长度。然后您可以找到c。最后,找到横截面圆的直径。
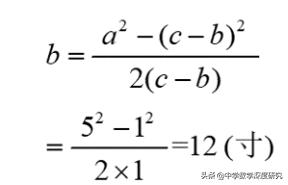
因此,C = B +(CB)= 12 + 1 = 13(英寸),直径= 2C = 26(英寸)。
以上是直接应用问题6中的公式来解决它。这很好!但是实际上,“九章算术”中对这个问题9的解决方案不是这样。我将在下面进行介绍。 “九章”中的解决方案是:“一半的锯方式乘以一个,例如深英寸,然后用深英寸增加,即材料的直径。”该方法实际上使用了我们现在正在谈论的内容:圆圈内的两条线由相交字符串形成的两个线段的产物相等(正确性可以通过相似的三角形证明)。也就是说,如果MN和PQ是两个在点S处相交的和弦,则MS·SN = PS·Sq。
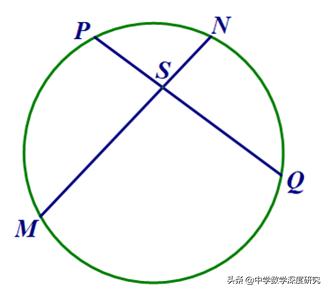
具体而言,如下图所示,“九章”中毕达哥拉斯章的第9个问题,有bc·ce = dc·cf,
现在
所以,
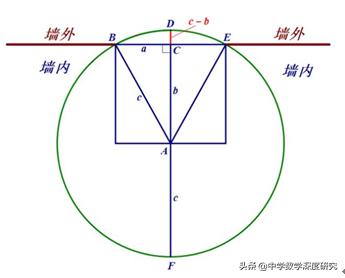
然后,添加C+B和CB以获得2C,即圆的直径。因此,如果直径为d,则
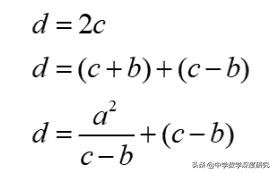
该公式是毕达哥拉斯章节中问题9中使用的方法:“一半的锯小径本身就乘以一英寸,然后将其增加一英寸,这意味着材料的直径。”
替换已知条件a = 5和cb = 1并获得d = 25/1+1 = 26(英寸),这与第一种方法的结果相同。
上述找到直径的公式是所谓的“ ARC-SAG公式”。一般来说,弧矢状公式如下:有弓形,其和弦长度为c(请注意,它与以前使用的C含义不同,以下B也不同),并且弧高度为b(如下图所示),然后弧位的圆的直径为d
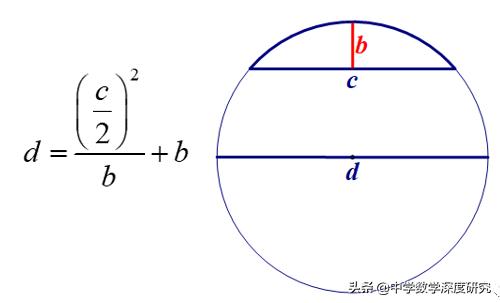
最后,有两个想法:
(1)我看到了许多中国古代建筑物中隐藏在墙壁上的柱子,揭示了一些圆柱体。使用“锯”方法似乎不好,因为不可能直接测量其直径。无论圆柱是什么,不建议通过“锯和锯子”损坏它。实际上还有许多其他测量方法。例如,您可以使用石膏制作凹形弧,当然,哪个弧度恰好夹在圆柱体表面上,然后我们可以测量该弧的直径。
(2)我们通常认为,上述问题中的圆形材料是圆柱形的。但是,并非不可能认为它是一个球形对象。对问题的解决方案与球的解决方案相同,而发现的直径是球的直径。
“这仍然不足,这是一个问题。”在小学中,已经有一个系统的解决方案解决了魔鬼的应用问题。例如:现在,有些人总共购买鸡,而六分之一的人中有六分之六的六分之一中有六分之六的六分之六的六分之六的六分之六的六分之六的人中有六分之六的人中有九分之六。人数和鸡的价格是多少?答案是:九个人,鸡的价格为七十。
让我们看一下如何在古代我的国家解决它:

今天的解决方案:假设人数为x,鸡的价格为y,然后y = 9x-11,y = 6x+16解决方案是x = 9 y = 70。
古代方法2更容易理解,因为它考虑了消除y。使用以下公式减去上述公式以获取3倍= 27以找到人数,然后替换以找到价格。
古代方法1,该过程有点复杂,但可以理解为我们消除X的想法,使用3x = 27,6y = 54x-66,9y = 54x+144,将其减去以获得3y = 210,y = 70。
从这个角度来看,我们的祖先还可以考虑相应的方法来解决问题,然后他们才知道设置未知数的想法。有时他们不欣赏古人的思想。他们本来可以在数百年甚至数千年前这样做的。提出这些方法。同时,随着时间的发展,我们的技术创新还产生了许多新的工具和方法来帮助我们解决问题,这也是时代进步给我们带来的好处。从一无所有到某物的过程是最困难的。我们可以学习并借用我们的前辈留给我们的知识的结晶,这也将促进时代的发展。
直到1675年,意大利数学书籍称这种方法为“中国算法”。在本书中,提到了直接分裂,这是世界上线性方程式完整系统的最早解决方案,本质上是矩阵的当前基本转换。本章也有负数,在国外,有一个说法是在7世纪第一。

Liu Hui为改善“算术九章”制度做出了巨大贡献,他是WEI和JIN王朝的一位伟大的数学家,也是中国古典数学理论的创始人之一。
他的数学成就大致分为两个方面:
首先,组织古老的数学系统并奠定理论基础。这一点主要反映在“算术注释的九章”中,包括数字系统,区域和音量理论等。他的第一个创造是现代基本算术中的分数的点,以及无限接近的想法小数分数的非理性根。
第二个是自己的创新,主要是在PI-Realization技术中。
西方人似乎首先使用了极限的象征,但实际上,在解决问题时,就已经有一个极限想法了。 Zhuangzi说的:“每天都可以将一只脚的脚拿走一半,这将永远是无穷无尽的。”已经有一种表达“无限少量”的想法。
最终的思想主要存在于“算术九章”中的“ fang tian”一章中,这是查找区域和数量的问题。
当Liu Hui对“算术的九章”进行注释时,他首先指出,先前的“三个直径”(即,π= 3)实际上是圆的周围和直径的比例这个声明。很粗糙。为了找到圆的面积公式(基本上是找到π),他开始不断切割圆圈。这是我们通常称为“圆形切割”的东西,这也是一个非常经典的极端想法。他本人说:“它越薄,越小,它越小,越小,切割越小,即使未切割,它也会与圆圈集成在一起,也会有没有损失。”

“算术的九章”决定了中国古代数学的框架,其计算特征是中心,与现实密切相关,并旨在解决人们的生产和生活中的数学问题。它的影响是如此深刻,以至于将来中国数学作品通常采用两种形式:为它们进行注释或以相同的形式写书;即使将西方算术介绍给中国,人们也经常将西方算术列入书籍及其理论。内部的数学知识包含在九个章节的框架中。
“算术九章”的意义远远超过其在中国数学史上的重要地位。它还反映出,在秦王朝期间,我国的古代数学在世界上取得了领先的发展。这个领导地位一直持续到公元14世纪初。
实际上,我们值得考虑的仔细考虑,在中国古代数学的辉煌成就与现代中国数学的缺乏成就之间存在问题。也许是由于缺乏公理系统导致较弱的证明逻辑的结果,也许这是中国古典数学中没有继任者的结果,或者也许是现代数学教育问题的结果。但是,无论如何,我们可以再次看到中国数学的兴起。
如果“几何形状的起源”是西方数学历史的发起人,并指导西方自然科学的发展,那么“算术的九章”(与“几何的起源”一样著名)自然就是起源于东部自然科学。






